What Is 6 To The Power Of 2
Kalali
Mar 28, 2025 · 5 min read
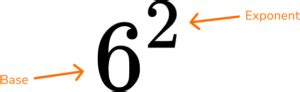
Table of Contents
What is 6 to the Power of 2? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What is 6 to the power of 2?" opens a door to a vast world of mathematical concepts and practical applications. While the answer itself is straightforward – 36 – understanding the underlying principles of exponents unlocks a powerful tool used across numerous fields, from simple calculations to complex scientific modeling. This article will delve into the meaning of exponents, explore the calculation of 6², and discuss its relevance in various contexts.
Understanding Exponents: The Power of Repeated Multiplication
Exponents, also known as powers or indices, represent repeated multiplication of a base number. The expression 6² (read as "6 to the power of 2" or "6 squared") signifies that the base number, 6, is multiplied by itself twice. In general, the expression bⁿ means that the base b is multiplied by itself n times.
Formula: bⁿ = b × b × b × ... × b (n times)
Therefore, 6² = 6 × 6 = 36.
This seemingly simple concept forms the foundation for many advanced mathematical operations and is crucial in various scientific and engineering disciplines.
Calculating 6²: A Step-by-Step Approach
Calculating 6² is straightforward, even without a calculator. Simply multiply 6 by itself:
- Step 1: Identify the base number (6).
- Step 2: Identify the exponent (2).
- Step 3: Multiply the base number by itself the number of times indicated by the exponent: 6 × 6 = 36.
Therefore, 6 to the power of 2 is 36.
Beyond 6²: Exploring Higher Powers and Negative Exponents
While 6² is a simple example, the concept of exponents extends to much larger numbers and even negative exponents. Let's briefly explore these:
-
Higher Powers: Consider 6³, which is 6 to the power of 3. This means 6 × 6 × 6 = 216. Similarly, 6⁴ = 6 × 6 × 6 × 6 = 1296, and so on. As the exponent increases, the result grows exponentially.
-
Negative Exponents: Negative exponents represent the reciprocal of the positive exponent. For example, 6⁻² is the reciprocal of 6², which is 1/6² = 1/36. In general, b⁻ⁿ = 1/bⁿ.
The Importance of Understanding Exponents: Real-World Applications
The concept of exponents isn't merely an abstract mathematical concept; it holds significant practical value across numerous fields. Here are some examples:
1. Area Calculation:
Calculating the area of a square is a classic application of exponents. If a square has a side length of 6 units, its area is 6² = 36 square units. This applies to numerous real-world scenarios, from calculating the area of a room to determining the surface area of a piece of land.
2. Volume Calculation:
Calculating the volume of a cube is another prime example. A cube with a side length of 6 units has a volume of 6³ = 216 cubic units. This is crucial in various applications, from packaging design to construction engineering.
3. Compound Interest:
In finance, compound interest calculations heavily rely on exponents. The formula for compound interest incorporates exponents to determine the future value of an investment based on the principal amount, interest rate, and compounding period. Understanding exponents is crucial for making informed financial decisions.
4. Scientific Notation:
Scientific notation uses exponents to represent extremely large or small numbers concisely. For example, the speed of light is approximately 3 × 10⁸ meters per second. The exponent 8 indicates that the number 3 is multiplied by 10 eight times, representing a very large number. This is essential in scientific fields like astronomy and physics.
5. Population Growth:
Modeling population growth often involves exponential functions. The growth can be described by an equation that incorporates exponents, allowing scientists to predict future population sizes based on current growth rates.
6. Radioactive Decay:
Radioactive decay follows an exponential decay pattern. The rate of decay is described using exponential functions, allowing scientists to determine the half-life of radioactive isotopes and predict the remaining amount of a radioactive substance over time.
7. Computer Science:
Exponents are fundamental in computer science, particularly in algorithms and data structures. Big O notation, which describes the efficiency of algorithms, often uses exponents to represent the growth rate of an algorithm's time or space complexity. Understanding exponents is critical for optimizing software performance.
8. Physics and Engineering:
Many physical phenomena, such as the intensity of light or sound, follow inverse square laws, which involve negative exponents. This is crucial for designing and optimizing various technologies.
Expanding on Exponents: Further Exploration
Beyond the basics, the world of exponents expands to include:
-
Fractional Exponents: Fractional exponents represent roots. For example, 6^(1/2) is the square root of 6, and 6^(1/3) is the cube root of 6.
-
Irrational Exponents: Exponents can also be irrational numbers, such as π or e. These are calculated using advanced mathematical techniques.
-
Complex Exponents: Exponents can even be complex numbers, involving both real and imaginary parts. This is a crucial concept in advanced mathematics and physics.
-
Logarithms: Logarithms are the inverse of exponents. They are used to solve equations involving exponents and have widespread applications in various fields, including chemistry, acoustics, and earthquake measurement.
Conclusion: The Power of Understanding 6² and Beyond
While the answer to "What is 6 to the power of 2?" is simply 36, the underlying concept of exponents is far more profound. Understanding exponents unlocks a powerful tool used across countless fields, enabling us to model complex phenomena, solve intricate problems, and make informed decisions. From calculating areas and volumes to understanding compound interest and modeling population growth, exponents are an essential component of numerous mathematical and scientific applications. Mastering this fundamental concept opens doors to a deeper understanding of the world around us. The seemingly simple 6² serves as a gateway to a vast and fascinating world of mathematical possibilities. Continued exploration into exponents will undoubtedly reveal even greater applications and deepen one's appreciation for their power and versatility.
Latest Posts
Latest Posts
-
How Many Inches Is 30 Ft
Mar 31, 2025
-
What Is The Boiling Point Of Saltwater
Mar 31, 2025
-
What Are The 2 Parts Of A Solution
Mar 31, 2025
-
What Are The Chemical Equations Of Photosynthesis And Cellular Respiration
Mar 31, 2025
-
What Is 57 Celsius In Fahrenheit
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is 6 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
