What Is 60 Percent Of 50
Kalali
Apr 17, 2025 · 5 min read
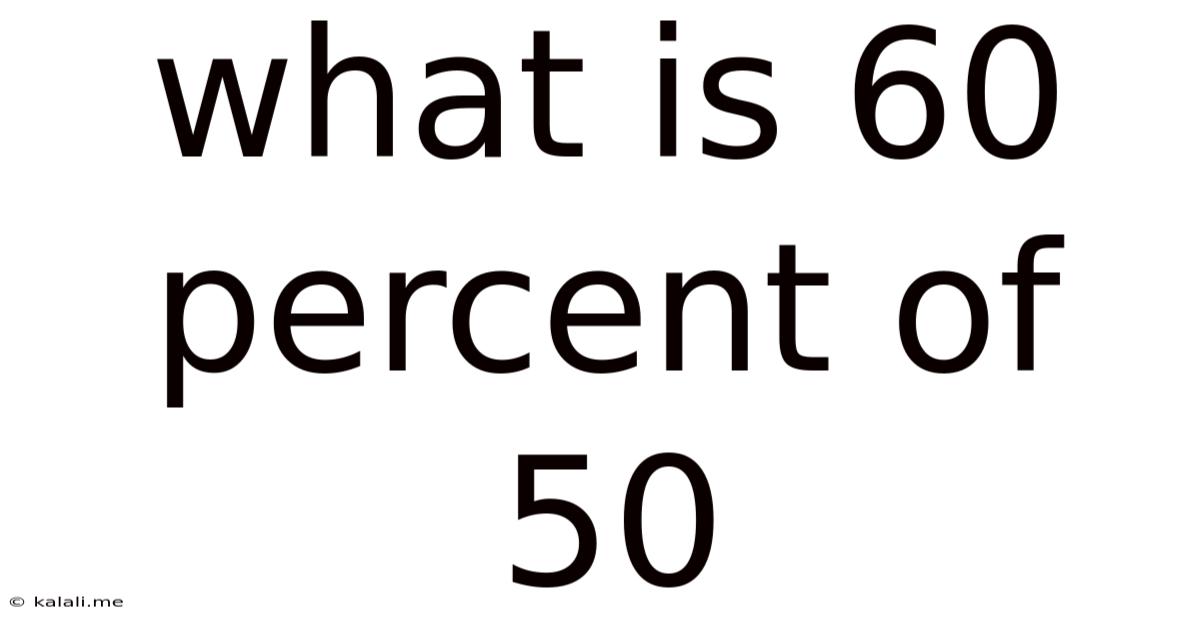
Table of Contents
What is 60 Percent of 50? A Deep Dive into Percentages and Their Applications
What is 60 percent of 50? The answer is simple: 30. But this seemingly straightforward calculation opens a door to a world of mathematical concepts with far-reaching applications in everyday life, from calculating discounts to understanding complex statistical analyses. This article will not only answer the initial question but will also delve into the underlying principles of percentages, exploring various methods for calculating them and highlighting their importance in different fields.
Meta Description: Learn how to calculate 60% of 50 and explore the broader world of percentages. This comprehensive guide covers various calculation methods, real-world applications, and the importance of percentages in different fields. Unlock the power of percentage calculations!
Understanding Percentages: The Foundation
A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" is derived from the Latin words "per centum," meaning "out of a hundred." Essentially, a percentage represents a portion of a whole. For example, 60% means 60 out of 100, or 60/100, which simplifies to 3/5. Understanding this fundamental concept is crucial for tackling any percentage-related problem. This includes understanding the relationship between percentages, decimals, and fractions, all of which are interchangeable representations of the same numerical value.
Calculating 60% of 50: Multiple Approaches
There are several ways to calculate 60% of 50. Let's explore the most common methods:
1. Using the Decimal Equivalent:
The most straightforward method involves converting the percentage to its decimal equivalent. To do this, simply divide the percentage by 100. In this case, 60% becomes 60/100 = 0.60. Then, multiply this decimal by the number you want to find the percentage of:
0.60 * 50 = 30
Therefore, 60% of 50 is 30. This method is widely used for its simplicity and efficiency.
2. Using Fractions:
As mentioned earlier, percentages can be expressed as fractions. 60% can be written as 60/100, which simplifies to 3/5. To find 60% of 50, multiply 50 by the fraction:
(3/5) * 50 = 30
This method is particularly useful when dealing with percentages that have simple fractional equivalents.
3. Using Proportion:
The concept of proportion provides another effective way to calculate percentages. Set up a proportion:
x/50 = 60/100
Cross-multiply and solve for x:
100x = 3000 x = 30
This method is helpful in understanding the relationship between the parts and the whole.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of life. Here are some examples:
-
Sales and Discounts: Retail stores frequently offer discounts expressed as percentages. For instance, a 20% discount on a $100 item means you'll pay $80 (100 - (20/100)*100). Understanding percentage calculations is crucial for smart shopping.
-
Taxes and Interest: Governments levy taxes on income, goods, and services, often expressed as percentages. Similarly, interest rates on loans and investments are typically stated as percentages.
-
Financial Analysis: Percentage change is a vital tool in financial analysis. It's used to track the growth or decline of investments, profits, and other financial metrics. For example, calculating the percentage increase or decrease in stock prices over a period is essential for investors.
-
Statistical Analysis: Percentages are extensively used in statistical analysis to represent proportions, frequencies, and probabilities. This includes analyzing survey data, market research, and scientific experiments. For instance, expressing the percentage of respondents who prefer a particular product helps in understanding consumer preferences.
-
Grading and Assessment: In education, grades are often expressed as percentages, reflecting a student's performance on tests, assignments, and projects.
-
Science and Engineering: Percentages are frequently used to represent concentrations, efficiencies, and errors in scientific and engineering calculations.
Beyond the Basics: Advanced Percentage Calculations
While calculating 60% of 50 is relatively straightforward, more complex percentage calculations might involve finding the percentage increase or decrease, calculating the original value before a percentage change, or working with multiple percentages simultaneously.
1. Percentage Increase/Decrease:
Calculating the percentage increase or decrease involves finding the difference between two values and expressing it as a percentage of the original value. The formula is:
[(New Value - Original Value) / Original Value] * 100
For example, if the price of an item increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] * 100 = 20%
2. Finding the Original Value:
If you know the final value after a percentage increase or decrease, you can work backward to find the original value. For instance, if an item costs $60 after a 20% increase, the original price can be calculated as follows:
Original Value = Final Value / (1 + Percentage Increase as Decimal)
Original Value = 60 / (1 + 0.20) = 50
3. Multiple Percentages:
When dealing with multiple percentage changes, it's crucial to remember that they don't simply add up. For example, a 10% increase followed by a 10% decrease does not result in the original value. Each percentage change is calculated sequentially.
Mastering Percentages: Tips and Tricks
-
Practice Regularly: The best way to master percentage calculations is through regular practice. Work through various examples and problems to build your confidence and understanding.
-
Use a Calculator: For more complex calculations, a calculator can be a valuable tool. Most calculators have a percentage function that simplifies the process.
-
Understand the Concepts: Don't just memorize formulas; understand the underlying concepts. This will make it easier to apply percentage calculations in different contexts.
-
Break Down Complex Problems: If you encounter a complex problem, break it down into smaller, more manageable steps.
-
Check Your Work: Always double-check your answers to ensure accuracy.
Conclusion: The Importance of Percentage Proficiency
The ability to calculate percentages accurately and efficiently is a valuable skill with widespread applications. From navigating everyday financial transactions to understanding complex data analyses, a strong grasp of percentage calculations empowers individuals to make informed decisions and succeed in various fields. While the answer to "What is 60 percent of 50?" is simply 30, understanding the underlying principles and broader applications of percentage calculations is what truly matters. By mastering these concepts, you equip yourself with a powerful tool for success in a data-driven world. So, next time you encounter a percentage calculation, remember the fundamentals and approach the problem systematically, applying the appropriate method to reach the correct and confident solution.
Latest Posts
Latest Posts
-
How Much Feet Is 44 Inches
Apr 19, 2025
-
What Is An 8 Out Of 12
Apr 19, 2025
-
What Percentage Is 12 Out Of 14
Apr 19, 2025
-
What Is The Decimal For 9 20
Apr 19, 2025
-
2 Out Of 5 In Percentage
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 60 Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.