What Is The Decimal For 9/20
Kalali
Apr 19, 2025 · 5 min read
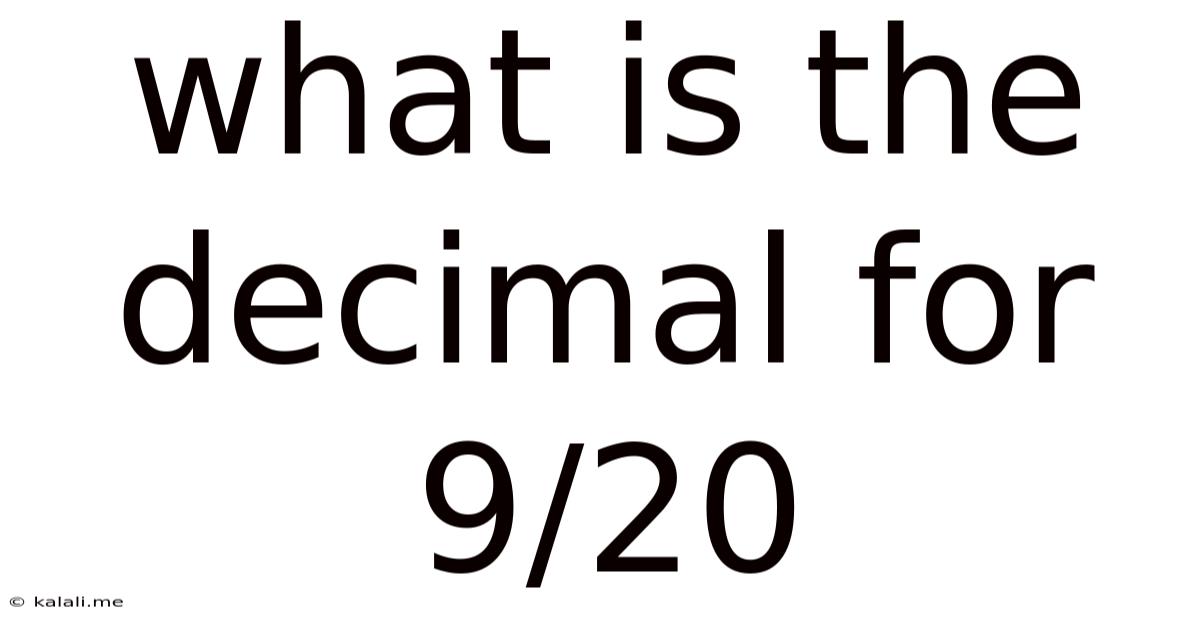
Table of Contents
What is the Decimal for 9/20? A Deep Dive into Fraction-to-Decimal Conversion
This article explores the simple yet fundamental conversion of the fraction 9/20 into its decimal equivalent. While the answer itself is straightforward, we'll delve deeper into the underlying principles, exploring various methods for fraction-to-decimal conversion and highlighting their applications in different contexts. This will provide a comprehensive understanding not just of this specific conversion, but of the broader concept of representing numbers in different numerical systems. The meta description is: Learn how to convert fractions to decimals, using 9/20 as an example. We cover different methods, explore practical applications, and discuss the importance of understanding numerical representation.
Understanding Fractions and Decimals
Before jumping into the conversion, let's solidify our understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, and the denominator indicates how many parts make up the whole.
A decimal, on the other hand, represents a number using a base-10 system, where each digit to the right of the decimal point represents a power of 10 (tenths, hundredths, thousandths, and so on). Decimals provide a concise way to represent fractions and other numbers.
Method 1: Direct Division
The most straightforward method to convert a fraction to a decimal is through direct division. We divide the numerator by the denominator. In the case of 9/20:
9 ÷ 20 = 0.45
Therefore, the decimal equivalent of 9/20 is 0.45. This method is universally applicable and easy to perform using a calculator or through manual long division. Understanding long division is crucial for building a solid foundation in mathematics and for situations where a calculator isn't readily available. This method is particularly useful for fractions with relatively small numerators and denominators.
Method 2: Converting to an Equivalent Fraction with a Denominator of a Power of 10
This method leverages the fact that decimals are based on powers of 10. If we can convert the fraction into an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.), the decimal representation becomes immediately apparent.
Let's try this with 9/20. We need to find a number we can multiply the denominator (20) by to obtain a power of 10. Since 20 x 5 = 100, we can use this:
(9 x 5) / (20 x 5) = 45/100
Now, 45/100 is easily converted to a decimal. The denominator, 100, represents hundredths, so the numerator, 45, represents 45 hundredths. Therefore:
45/100 = 0.45
This method provides a clear visual representation of the decimal value and reinforces the understanding of place value in the decimal system. It's particularly helpful for fractions whose denominators are easily converted to powers of 10, such as those with denominators that are factors of 10, 100, or 1000. This method strengthens the conceptual understanding of equivalent fractions.
Method 3: Using a Calculator
In today's digital age, calculators are readily available, providing a quick and efficient way to convert fractions to decimals. Simply input the fraction as 9 ÷ 20, and the calculator will display the decimal equivalent, 0.45. While convenient, it's crucial to understand the underlying mathematical principles to troubleshoot potential issues and to build a strong mathematical intuition. Over-reliance on calculators can hinder the development of essential mathematical skills.
Practical Applications of Fraction-to-Decimal Conversions
The conversion of fractions to decimals has wide-ranging applications across various fields:
-
Finance: Calculating percentages, interest rates, and profit margins often involves converting fractions to decimals. For example, a 9/20 discount can be easily calculated as 0.45 times the original price.
-
Engineering and Science: In engineering and scientific calculations, decimals are preferred for their ease of use in computations and their accuracy in representing measurements. For instance, representing the proportion of a material in a mixture.
-
Data Analysis and Statistics: Data representation and statistical calculations often involve decimals for ease of computation and interpretation. Fractions can often be less intuitive to analyze.
-
Everyday Life: Many everyday situations involve using decimals, such as calculating tips, measuring ingredients in recipes, or determining distances.
Understanding the Significance of Decimal Representation
The conversion from fractions to decimals highlights the flexibility and versatility of numerical representation. Different contexts demand different representations. While fractions offer a clear representation of parts of a whole, decimals provide a convenient format for calculations and comparisons, especially in the context of larger datasets or complex computations. Mastering both fraction and decimal representations provides a powerful toolkit for problem-solving across various disciplines.
Beyond 9/20: Expanding the Concept
While this article focused on converting 9/20, the principles discussed are applicable to converting any fraction to a decimal. The key is understanding the relationship between the numerator and the denominator and choosing the most appropriate conversion method based on the specific fraction. For fractions with recurring decimals, understanding the concept of repeating decimals becomes crucial.
Recurring Decimals and their Representation
Some fractions, when converted to decimals, result in non-terminating, repeating decimals. For example, 1/3 converts to 0.3333... These repeating decimals are often represented using a bar over the repeating digits (e.g., 0.3̅). Understanding how to convert fractions to both terminating and recurring decimals is essential for a comprehensive understanding of numerical representation. This further emphasizes the importance of understanding both fraction and decimal representations and their inter-relation.
Conclusion: The Power of Numerical Fluency
The seemingly simple conversion of 9/20 to 0.45 highlights the power of numerical fluency and the importance of understanding different numerical representations. Mastering fraction-to-decimal conversions is a foundational skill with wide-ranging applications, from everyday calculations to complex scientific computations. By understanding the different methods and their underlying principles, we gain a deeper appreciation for the versatility and power of numbers in various contexts. This foundational understanding allows for greater efficiency and accuracy in problem-solving and mathematical reasoning across diverse fields. The ability to seamlessly transition between fractions and decimals is a significant asset in any numerical task.
Latest Posts
Latest Posts
-
1 Pint Is How Many Milliliters
Apr 20, 2025
-
16 Over 5 As A Mixed Number
Apr 20, 2025
-
What Is 114 Cm In Inches
Apr 20, 2025
-
4 Meters Equals How Many Feet
Apr 20, 2025
-
How Many 1 3 Are In 1 Cup
Apr 20, 2025
Related Post
Thank you for visiting our website which covers about What Is The Decimal For 9/20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.