What Is 9 16 As A Decimal
Kalali
Mar 28, 2025 · 5 min read
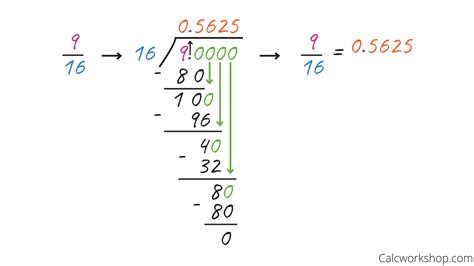
Table of Contents
What is 9/16 as a Decimal? A Comprehensive Guide to Fraction-to-Decimal Conversion
Converting fractions to decimals is a fundamental skill in mathematics with broad applications in various fields. This comprehensive guide will delve into the process of converting the fraction 9/16 into its decimal equivalent, exploring different methods and providing a solid understanding of the underlying principles. We'll also explore related concepts and applications to enhance your mathematical proficiency.
Understanding Fractions and Decimals
Before we dive into the conversion of 9/16, let's briefly review the core concepts of fractions and decimals.
-
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts, while the numerator indicates the number of parts being considered.
-
Decimals: A decimal is another way to represent a part of a whole. It uses a base-10 system, where the digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on.
Method 1: Long Division
The most straightforward method to convert a fraction to a decimal is through long division. In this method, we divide the numerator (9) by the denominator (16).
-
Set up the division: Write 9 as the dividend (inside the division symbol) and 16 as the divisor (outside the division symbol). Add a decimal point followed by zeros to the dividend to facilitate the division process.
16 | 9.0000 -
Perform the division: Start dividing 16 into 90. 16 goes into 90 five times (16 x 5 = 80). Write 5 above the 0 in the quotient.
0.5 16 | 9.0000 -80 10 -
Bring down the next digit: Bring down the next digit (0) to create 100.
-
Continue the division: 16 goes into 100 six times (16 x 6 = 96). Write 6 above the next 0 in the quotient.
0.56 16 | 9.0000 -80 100 -96 4 -
Repeat the process: Bring down another zero to create 40. 16 goes into 40 two times (16 x 2 = 32). Write 2 above the next 0.
0.562 16 | 9.0000 -80 100 -96 40 -32 8 -
Continue until you reach a repeating pattern or desired accuracy: Bring down another zero to create 80. 16 goes into 80 five times. The pattern will repeat.
0.5625 16 | 9.0000 -80 100 -96 40 -32 80 -80 0
Therefore, 9/16 as a decimal is 0.5625.
Method 2: Converting to an Equivalent Fraction with a Denominator of a Power of 10
While long division is reliable, this method is sometimes faster, particularly when dealing with fractions that have denominators that can easily be converted to powers of 10 (10, 100, 1000, etc.). Unfortunately, 16 is not easily converted to a power of 10. However, understanding this method is valuable for other fractions. To use this method, we would need to find a number to multiply both the numerator and denominator to produce a denominator that's a power of 10. In this case, there isn't a whole number that can achieve this directly.
Method 3: Using a Calculator
Modern calculators readily perform fraction-to-decimal conversions. Simply enter the fraction 9/16 and press the "equals" button. The calculator will display the decimal equivalent, 0.5625.
Applications of Decimal Conversions
The ability to convert fractions to decimals is crucial in various real-world applications:
-
Financial Calculations: Calculating interest rates, discounts, and profit margins often involve working with fractions and decimals.
-
Engineering and Design: Precision measurements and calculations in engineering and design rely heavily on decimal representation.
-
Scientific Calculations: Many scientific formulas and measurements use decimal numbers.
-
Data Analysis: In statistics and data analysis, decimals are essential for representing proportions and percentages.
-
Everyday Life: Dividing food equally amongst friends, measuring ingredients for cooking, calculating unit prices at the store, and understanding percentages on sale signs are all common examples of how decimals are used in everyday life.
Understanding Repeating and Terminating Decimals
When converting fractions to decimals, you may encounter two types of decimals:
-
Terminating Decimals: These decimals have a finite number of digits after the decimal point. For example, 9/16 = 0.5625 is a terminating decimal.
-
Repeating Decimals: These decimals have a pattern of digits that repeats infinitely after the decimal point. For instance, 1/3 = 0.3333... The digit 3 repeats indefinitely.
The type of decimal obtained depends on the denominator of the fraction. If the denominator only contains the prime factors 2 and 5 (or is a power of 10), the resulting decimal will be terminating. Otherwise, the decimal will be repeating. Since 16 = 2<sup>4</sup>, 9/16 results in a terminating decimal.
Further Exploration: Working with More Complex Fractions
The principles discussed above can be applied to convert any fraction to a decimal, regardless of the complexity of the numerator and denominator. For example, let's consider a more complex fraction like 27/64. Applying long division or using a calculator, you'd find that 27/64 equals 0.421875. This is another terminating decimal because 64 = 2<sup>6</sup>.
Conclusion:
Converting 9/16 to its decimal equivalent is a straightforward process achievable through long division, calculator use, or (less efficiently in this case) by converting to an equivalent fraction with a denominator that is a power of 10. The result, 0.5625, is a terminating decimal. Understanding this process is vital for numerous applications across various disciplines and everyday life, highlighting the importance of mastering this fundamental mathematical skill. Practice converting different fractions to decimals to build confidence and proficiency in this crucial aspect of mathematics. Remember to explore the different methods to find the approach that works best for you.
Latest Posts
Latest Posts
-
How Many Ounces In A Cup And Half
Mar 31, 2025
-
Cuanto Es 37 Grados Centigrados En Fahrenheit
Mar 31, 2025
-
90 Cm Equals How Many Inches
Mar 31, 2025
-
Cuanto Es Un Acre En Pies
Mar 31, 2025
-
What Is The Least Common Multiple Of 7 And 9
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is 9 16 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
