What Is A Common Multiple Of 8 And 10
Kalali
Mar 28, 2025 · 5 min read
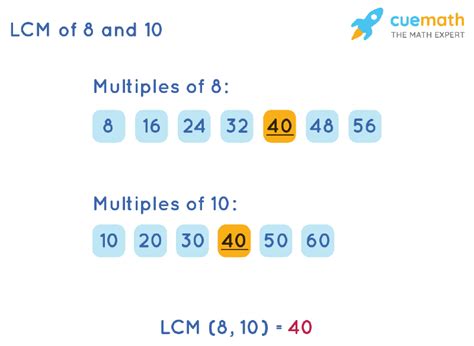
Table of Contents
What is a Common Multiple of 8 and 10? A Deep Dive into Number Theory
Finding the common multiples of two numbers might seem like a simple mathematical task, but understanding the underlying principles reveals a fascinating glimpse into number theory. This article delves deep into the concept of common multiples, focusing specifically on the common multiples of 8 and 10. We'll explore various methods for finding these multiples, explain the significance of least common multiples (LCM), and touch upon their applications in real-world scenarios.
Understanding Multiples
Before diving into common multiples, let's establish a firm grasp on the concept of multiples itself. A multiple of a number is the result of multiplying that number by any integer (a whole number, including zero, negative numbers, and positive numbers).
For example, the multiples of 8 are: 0, 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, and so on, extending infinitely in both positive and negative directions. Similarly, the multiples of 10 are: 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, and so on, again extending infinitely.
Identifying Common Multiples of 8 and 10
A common multiple of two or more numbers is a number that is a multiple of all the given numbers. In our case, we're looking for the common multiples of 8 and 10. To find these, we can list out the multiples of each number and identify the ones that appear in both lists:
Multiples of 8: 0, 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128...
Multiples of 10: 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130...
Notice that several numbers appear in both lists: 0, 40, 80, 120, and so on. These are the common multiples of 8 and 10. This method works well for smaller numbers but becomes cumbersome as the numbers get larger.
The Least Common Multiple (LCM)
Among the infinite set of common multiples, the least common multiple (LCM) holds particular significance. The LCM is the smallest positive common multiple of two or more numbers, excluding zero. In our example, the LCM of 8 and 10 is 40.
Finding the LCM is crucial in various mathematical problems and real-world applications, as we will explore later.
Methods for Finding the LCM
Several methods can efficiently determine the LCM of two or more numbers. Let's explore two common approaches:
1. Listing Multiples Method (Suitable for smaller numbers):
As demonstrated earlier, this involves listing the multiples of each number until a common multiple is found. This method is straightforward but less efficient for larger numbers.
2. Prime Factorization Method (Efficient for larger numbers):
This method leverages the prime factorization of each number. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 10: 2 x 5
To find the LCM using prime factorization:
- Identify all prime factors: The prime factors are 2 and 5.
- Take the highest power of each prime factor: The highest power of 2 is 2³ (from the factorization of 8), and the highest power of 5 is 5¹ (from the factorization of 10).
- Multiply the highest powers together: 2³ x 5 = 8 x 5 = 40
Therefore, the LCM of 8 and 10 is 40, confirming our earlier findings. This method is far more efficient than listing multiples, particularly when dealing with larger numbers.
Applications of LCM
The concept of LCM finds practical applications in various fields:
-
Scheduling: Imagine two buses departing from the same station, one every 8 minutes and the other every 10 minutes. The LCM (40 minutes) determines when both buses will depart simultaneously again.
-
Fraction Operations: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential to find a common denominator. This simplifies the calculations.
-
Measurement Conversions: Converting between different units of measurement often involves using the LCM to find the smallest common unit.
-
Project Management: In project management, the LCM can help schedule tasks that depend on each other, ensuring optimal efficiency.
-
Construction and Engineering: The LCM plays a vital role in ensuring proper alignment and coordination in various construction and engineering projects. For instance, in designing structures with repeating patterns, the LCM can ensure consistent spacing.
-
Music Theory: LCM is used in determining the least common denominator when dealing with different rhythmic patterns or time signatures in music.
Beyond the LCM: Other Common Multiples
While the LCM is the smallest positive common multiple, there are infinitely many other common multiples. All common multiples of 8 and 10 are multiples of the LCM (40). Therefore, the common multiples are 0, 40, 80, 120, 160, and so on, extending infinitely.
Conclusion
Understanding the concept of common multiples, particularly the LCM, is fundamental to various mathematical applications and real-world problems. While listing multiples is a simple approach for smaller numbers, the prime factorization method offers a far more efficient solution for larger numbers. The LCM’s usefulness extends beyond the mathematical realm, finding practical applications in scheduling, fraction operations, measurement conversions, project management, and various other fields. By mastering the techniques presented in this article, you'll gain a deeper appreciation for the interconnectedness of seemingly simple mathematical concepts and their broad impact on our daily lives. The seemingly straightforward question, "What is a common multiple of 8 and 10?" unlocks a wealth of knowledge and practical skills within the fascinating world of number theory.
Latest Posts
Latest Posts
-
What Part Of The Plant Produces Food For The Plant
Mar 31, 2025
-
Water Is Always A Product In What Type Of Reaction
Mar 31, 2025
-
How Much Is A Half A Pint In Cups
Mar 31, 2025
-
Convert 18 Degrees C To Fahrenheit
Mar 31, 2025
-
What Is 33 C In Fahrenheit
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is A Common Multiple Of 8 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
