What Is Lcm Of 5 And 6
Kalali
Apr 06, 2025 · 5 min read
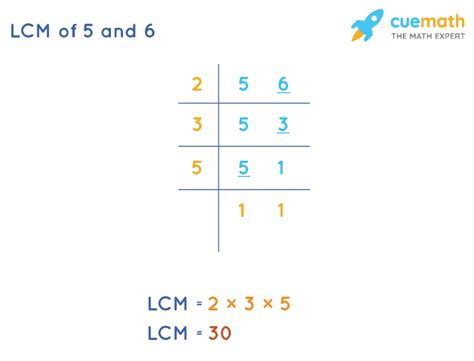
Table of Contents
What is the LCM of 5 and 6? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex equations. This article will thoroughly explore how to calculate the LCM of 5 and 6, examining multiple methods and delving into the underlying principles. We'll also explore the broader context of LCMs, highlighting their practical significance and applications in different fields.
Understanding Least Common Multiples (LCM)
Before diving into the specific calculation for 5 and 6, let's solidify our understanding of LCMs. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. This means it's a common multiple, but the smallest one.
For example, consider the numbers 2 and 3. Multiples of 2 are: 2, 4, 6, 8, 10, 12, 14, 16... Multiples of 3 are: 3, 6, 9, 12, 15, 18... Notice that 6 and 12 are common multiples. However, 6 is the least common multiple (LCM) of 2 and 3.
Methods for Calculating LCM(5, 6)
We can calculate the LCM of 5 and 6 using several different methods. Let's explore the most common ones:
1. Listing Multiples Method
This is a straightforward method, especially useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35...
- Multiples of 6: 6, 12, 18, 24, 30, 36...
The smallest number that appears in both lists is 30. Therefore, the LCM(5, 6) = 30.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the concept. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
- Prime factorization of 5: 5 (5 is a prime number)
- Prime factorization of 6: 2 x 3
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations and multiply them together. In this case:
LCM(5, 6) = 2 x 3 x 5 = 30
This method is particularly valuable when dealing with multiple numbers or larger numbers, as it provides a systematic approach to finding the LCM.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of two numbers are related through the following formula:
LCM(a, b) x GCD(a, b) = a x b
First, let's find the GCD of 5 and 6. Since 5 is a prime number and 6 is not divisible by 5, the GCD(5, 6) = 1.
Now, using the formula:
LCM(5, 6) x GCD(5, 6) = 5 x 6 LCM(5, 6) x 1 = 30 LCM(5, 6) = 30
This method is efficient when the GCD is easily determined, especially for larger numbers where prime factorization might be more time-consuming.
Applications of LCM in Real-World Scenarios
The concept of LCM isn't just confined to theoretical mathematics; it has various practical applications in different fields:
1. Scheduling and Time Management
Imagine two buses arrive at a bus stop at different intervals. One bus arrives every 5 minutes, and the other every 6 minutes. To find out when both buses will arrive at the bus stop simultaneously, we need to find the LCM(5, 6). The LCM, 30, signifies that both buses will arrive together every 30 minutes. This concept extends to various scheduling problems, from production lines to appointment scheduling.
2. Fraction Operations
LCM plays a crucial role in adding or subtracting fractions with different denominators. To add fractions like 1/5 and 1/6, we first need to find a common denominator, which is the LCM of the denominators (5 and 6). In this case, the LCM is 30. We then rewrite the fractions with the common denominator: 6/30 + 5/30 = 11/30.
3. Cyclic Patterns and Repetition
LCM is useful in identifying when cyclical events will coincide. For example, if two planets orbit a star with periods of 5 and 6 years respectively, the LCM(5, 6) = 30 indicates that both planets will be at their starting positions simultaneously every 30 years.
4. Music and Rhythm
In music, LCM helps determine the least common denominator for rhythmic patterns. If a musical phrase has a length of 5 beats and another phrase has a length of 6 beats, the LCM (30) helps determine the smallest length of time that encompasses both phrases without interruption.
Extending the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. The prime factorization method remains particularly useful. For instance, to find the LCM of 5, 6, and 10:
- Prime factorization of 5: 5
- Prime factorization of 6: 2 x 3
- Prime factorization of 10: 2 x 5
LCM(5, 6, 10) = 2 x 3 x 5 = 30
The listing multiples method becomes less practical with more numbers, while the GCD method would require using the GCD of multiple numbers iteratively.
Conclusion: The Significance of LCM(5, 6) = 30
The seemingly simple calculation of the LCM of 5 and 6 – resulting in 30 – underlies various important mathematical concepts and practical applications. Understanding the different methods for calculating LCMs equips us with the tools to tackle more complex problems involving multiples and common denominators. From scheduling tasks to simplifying fractions and understanding cyclic patterns, the LCM is a fundamental concept with wide-ranging implications in numerous fields. The ability to efficiently calculate LCMs enhances problem-solving skills and provides valuable insights in various practical scenarios. This deep dive has highlighted the importance of mastering this seemingly simple mathematical operation.
Latest Posts
Latest Posts
-
How Many Parallel Sides Does A Rhombus Have
Apr 08, 2025
-
2 Out Of 6 Is What Percent
Apr 08, 2025
-
How Many Liters Are In 1000 Milliliters
Apr 08, 2025
-
How Many Grams Is 150 Mg
Apr 08, 2025
-
The Ankle Is A Third Class Lever
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Is Lcm Of 5 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.