What Is Terminal Side Of The Angle
Kalali
Apr 06, 2025 · 6 min read
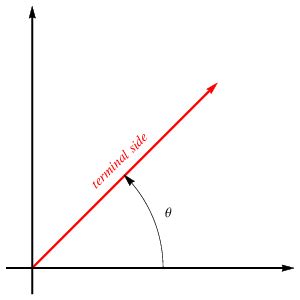
Table of Contents
What is the Terminal Side of an Angle? A Comprehensive Guide
Understanding the terminal side of an angle is fundamental to mastering trigonometry and its applications. This comprehensive guide will delve deep into this concept, providing clear explanations, helpful visualizations, and practical examples to solidify your understanding. We'll explore its definition, its role in different coordinate systems, and how it's used in various trigonometric calculations.
Defining the Terminal Side of an Angle
An angle is formed by two rays sharing a common endpoint, called the vertex. One ray is the initial side, typically positioned along the positive x-axis. The other ray is the terminal side, which rotates around the vertex to form the angle. The measure of the angle is determined by the amount of rotation from the initial side to the terminal side.
Think of it like the hands of a clock. The initial side is like the hour hand at 12 o'clock (pointing along the positive x-axis), and the terminal side is like the minute hand, which can rotate to any position, defining the angle formed.
Crucially: The terminal side's position determines the angle's value. Whether the rotation is clockwise (negative angle) or counterclockwise (positive angle) significantly impacts the terminal side's location and the angle's trigonometric values.
Visualizing the Terminal Side
Imagine a coordinate plane. The initial side always starts at the positive x-axis (0 degrees or 0 radians). Now, consider different angle measures:
-
Positive Angle (Counterclockwise Rotation): A positive angle measure indicates a counterclockwise rotation from the initial side. The terminal side will move counterclockwise around the origin.
-
Negative Angle (Clockwise Rotation): A negative angle measure indicates a clockwise rotation from the initial side. The terminal side will move clockwise around the origin.
-
Angles Greater than 360° (or 2π radians): If the angle measure exceeds a full rotation (360° or 2π radians), the terminal side will complete one or more full rotations before settling at its final position. The terminal side's position for 390°, for instance, is identical to that of 30° because 390° - 360° = 30°.
-
Angles Measured in Radians: The concepts remain the same whether angles are measured in degrees or radians. Remember that 360° equals 2π radians.
The Terminal Side and Trigonometric Functions
The terminal side's position is absolutely critical in determining the values of trigonometric functions (sine, cosine, and tangent). These functions relate the angle to the coordinates of a point on the terminal side.
Consider a point (x, y) on the terminal side of an angle θ, at a distance r from the origin. Then:
- cos θ = x/r (the x-coordinate divided by the distance from the origin)
- sin θ = y/r (the y-coordinate divided by the distance from the origin)
- tan θ = y/x (the y-coordinate divided by the x-coordinate)
The signs of these functions depend entirely on which quadrant the terminal side lies in.
Quadrantal Angles and the Terminal Side
Quadrantal angles are angles whose terminal side lies on one of the coordinate axes (0°, 90°, 180°, 270°, and 360° or their radian equivalents). For these angles, at least one of the x or y coordinates will be zero, leading to some trigonometric functions being undefined (division by zero).
Finding the Terminal Side: Examples
Let's work through some examples to illustrate finding the terminal side:
Example 1: Finding the Terminal Side of a 135° Angle
-
Start at the initial side: Place your initial side along the positive x-axis.
-
Rotate counterclockwise: Since the angle is positive (135°), rotate counterclockwise 135° from the positive x-axis.
-
Locate the terminal side: The terminal side will end up in the second quadrant, forming a 45° angle with the negative x-axis.
Example 2: Finding the Terminal Side of a -210° Angle
-
Start at the initial side: Begin at the positive x-axis.
-
Rotate clockwise: A negative angle signifies a clockwise rotation. Rotate 210° clockwise from the positive x-axis.
-
Locate the terminal side: The terminal side will lie in the second quadrant, forming a 30° angle with the positive x-axis. Note that -210° is coterminal with 150° (360° - 210° = 150°).
Example 3: Coterminal Angles and the Terminal Side
Coterminal angles share the same terminal side. For example, 30°, 390°, and -330° are coterminal angles because their terminal sides all occupy the same position. Adding or subtracting multiples of 360° (or 2π radians) will always result in a coterminal angle with the same terminal side.
Applications of the Terminal Side
The concept of the terminal side isn't just a theoretical construct; it's crucial for numerous applications:
-
Trigonometry: The foundation of trigonometry relies heavily on the position of the terminal side for calculating trigonometric ratios.
-
Vector Analysis: Vectors can be represented using angles and magnitudes, with the terminal side indicating the vector's direction.
-
Physics and Engineering: Analyzing projectile motion, rotational mechanics, and oscillatory systems often involves determining the position of the terminal side based on angle measurements.
-
Navigation and Surveying: Determining distances and directions using angles and coordinates relies fundamentally on understanding the terminal side's position.
-
Computer Graphics: In computer graphics, transformations, rotations, and positioning of objects in 2D and 3D space are often handled through angle calculations involving the terminal side.
Advanced Concepts Related to the Terminal Side
-
Unit Circle: The unit circle (a circle with a radius of 1 centered at the origin) is an invaluable tool for visualizing angles and their terminal sides. The coordinates of the point where the terminal side intersects the unit circle directly provide the cosine and sine values of the angle.
-
Reference Angles: The reference angle is the acute angle formed between the terminal side and the x-axis. Understanding reference angles simplifies trigonometric calculations, as trigonometric values for angles outside the first quadrant can be expressed in terms of their reference angle.
-
Trigonometric Identities: Many trigonometric identities rely on the relationships between angles and their terminal sides in different quadrants.
Conclusion
The terminal side of an angle is a cornerstone of trigonometry and its numerous applications. Mastering this concept is essential for success in various fields, from mathematics and physics to computer science and engineering. By understanding the relationship between angle measure, rotation, quadrant location, and the consequent trigonometric values, you'll unlock a deeper understanding of angles and their roles in solving complex problems. Remember the key points: the initial side starts at the positive x-axis, the rotation determines the terminal side's location, and the terminal side's position dictates the values of trigonometric functions. Through continued practice and visualization, you can solidify your grasp of this vital concept.
Latest Posts
Latest Posts
-
Fungi Have Cell Walls Made Of Peptidoglycan
Apr 06, 2025
-
5 Feet 5 Inches Is How Many Centimeters
Apr 06, 2025
-
Reacts With Water Physical Or Chemical Property
Apr 06, 2025
-
Distance Between Two Points In Polar Coordinates
Apr 06, 2025
-
How Long Is 70 Cm In Inches
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is Terminal Side Of The Angle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.