What Is The Gcf Of 12 And 18
Kalali
Mar 29, 2025 · 5 min read
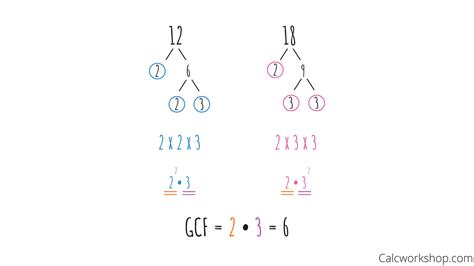
Table of Contents
What is the GCF of 12 and 18? A Deep Dive into Greatest Common Factors
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods involved provides a solid foundation for more advanced mathematical concepts. This article delves into the question, "What is the GCF of 12 and 18?", exploring multiple approaches to solving this problem and expanding upon the broader significance of GCFs in mathematics.
Understanding Greatest Common Factors (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that fits perfectly into both numbers. For example, if we consider the numbers 12 and 18, we are looking for the largest number that divides evenly into both 12 and 18.
This concept is crucial in various areas of mathematics, including:
- Simplifying fractions: Finding the GCF allows you to reduce fractions to their simplest form.
- Algebra: GCF is essential in factoring algebraic expressions.
- Geometry: GCF can help in solving problems involving lengths, areas, and volumes.
- Number theory: GCF is a fundamental concept in advanced number theory studies.
Methods for Finding the GCF of 12 and 18
Several methods can be used to determine the GCF of 12 and 18. Let's explore the most common ones:
1. Listing Factors
This is a straightforward method, particularly useful for smaller numbers. We list all the factors of each number and identify the largest common factor.
Factors of 12: 1, 2, 3, 4, 6, 12 Factors of 18: 1, 2, 3, 6, 9, 18
Comparing the lists, we see that the common factors are 1, 2, 3, and 6. The largest among them is 6. Therefore, the GCF of 12 and 18 is 6.
2. Prime Factorization
This method involves expressing each number as a product of its prime factors. The GCF is then found by multiplying the common prime factors raised to their lowest powers.
Prime factorization of 12: 2² × 3 Prime factorization of 18: 2 × 3²
The common prime factors are 2 and 3. The lowest power of 2 is 2¹ (or simply 2), and the lowest power of 3 is 3¹. Therefore, the GCF is 2 × 3 = 6.
3. Euclidean Algorithm
The Euclidean algorithm is a more efficient method for finding the GCF of larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 12 and 18:
- 18 - 12 = 6
- Now we find the GCF of 12 and 6.
- 12 - 6 = 6
- Since both numbers are now 6, the GCF is 6.
Why is understanding GCF important? Real-world Applications
Beyond the mathematical classroom, understanding GCFs has practical applications in several real-world scenarios:
-
Dividing resources equally: Imagine you have 12 apples and 18 oranges, and you want to divide them into equal groups for your friends. Finding the GCF (6) tells you that you can create 6 equal groups, each containing 2 apples and 3 oranges.
-
Simplifying measurements: In construction or design, you might need to cut pieces of wood or fabric into equal sizes. Knowing the GCF helps determine the largest possible size for these pieces without wasting material.
-
Scheduling events: If you have two events that occur every 12 days and 18 days respectively, the GCF will tell you how many days it will take for both events to coincide again. In this case, it's 6 days.
-
Data organization: In computer science, understanding GCF can be helpful when optimizing data structures or algorithms that require efficient division or grouping of data elements.
Expanding on GCF: Least Common Multiple (LCM)
Closely related to the GCF is the least common multiple (LCM). While the GCF is the largest number that divides both numbers, the LCM is the smallest number that is a multiple of both numbers.
Finding the LCM is often done in conjunction with finding the GCF. There's a useful relationship between the GCF and LCM of two numbers (a and b):
LCM(a, b) × GCF(a, b) = a × b
In our example, we know the GCF(12, 18) = 6. Therefore:
LCM(12, 18) × 6 = 12 × 18 LCM(12, 18) = (12 × 18) / 6 = 36
So, the LCM of 12 and 18 is 36.
Advanced Concepts Related to GCF
For those interested in delving deeper, here are some advanced concepts related to GCFs:
-
Bézout's Identity: This theorem states that for any two integers a and b, there exist integers x and y such that ax + by = GCF(a, b). This has applications in cryptography and other advanced mathematical fields.
-
Extended Euclidean Algorithm: This is an extension of the Euclidean algorithm that not only finds the GCF but also finds the integers x and y in Bézout's identity.
-
GCF in Polynomial Rings: The concept of GCF extends to polynomials, where we find the greatest common divisor of two or more polynomials.
Conclusion: Mastering GCFs for Mathematical Success
Understanding the concept of the greatest common factor (GCF) is fundamental to success in mathematics. Whether you're simplifying fractions, factoring expressions, or solving real-world problems, mastering different methods for finding the GCF will significantly enhance your mathematical skills. This article explored various approaches, from listing factors and prime factorization to the efficient Euclidean algorithm, and highlighted the practical applications of GCFs in various contexts. By understanding not only how to find the GCF but also why it's important, you'll build a strong foundation for more advanced mathematical concepts and problem-solving. Furthermore, understanding the relationship between GCF and LCM allows for a deeper comprehension of number theory and its applications. This knowledge is not just for academic purposes; it's a valuable tool applicable to numerous real-world situations, empowering you to solve problems more efficiently and effectively.
Latest Posts
Latest Posts
-
How Many Inches Is 25 Centimeters
Mar 31, 2025
-
How Long Is 2 Hours In Minutes
Mar 31, 2025
-
What Is 20 Of 70 Dollars
Mar 31, 2025
-
What Is 3 20 As A Percentage
Mar 31, 2025
-
1000 Km Is How Many Miles
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 12 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
