What Is The Lcm For 8 And 10
Kalali
Apr 03, 2025 · 5 min read
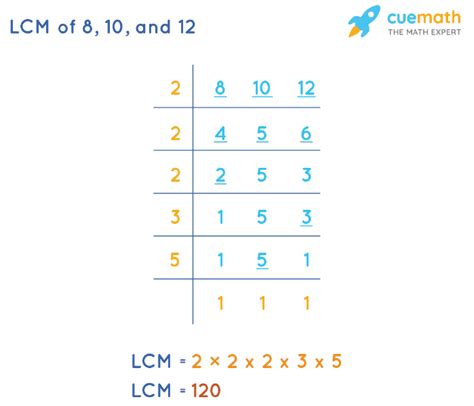
Table of Contents
What is the LCM for 8 and 10? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly useful in various fields like fractions, scheduling, and even music theory. This article will explore how to find the LCM for 8 and 10, covering multiple methods, providing practical examples, and delving into the underlying mathematical principles. We'll also discuss the importance of LCM in real-world applications and how understanding this concept can improve your mathematical skills.
Understanding Least Common Multiples (LCM)
Before we dive into calculating the LCM of 8 and 10, let's define what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For example, let's consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12... and the multiples of 3 are 3, 6, 9, 12, 15... The common multiples are 6, 12, 18... The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
The simplest method to find the LCM, particularly for smaller numbers, is by listing the multiples of each number until you find the smallest common multiple. Let's apply this to 8 and 10:
Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80...
Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100...
By comparing the lists, we can see that the smallest number that appears in both lists is 40. Therefore, the LCM of 8 and 10 is 40.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, is using prime factorization. This method involves breaking down each number into its prime factors. The prime factors are the prime numbers that, when multiplied together, result in the original number.
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 10: 2 x 5
To find the LCM using prime factorization:
- Identify all the prime factors: In this case, we have 2 and 5.
- Find the highest power of each prime factor: The highest power of 2 is 2³ (from the factorization of 8), and the highest power of 5 is 5¹ (from the factorization of 10).
- Multiply the highest powers together: 2³ x 5 = 8 x 5 = 40
Therefore, the LCM of 8 and 10 is 40 using the prime factorization method. This method is generally preferred for larger numbers as it's more systematic and less prone to errors.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the Greatest Common Divisor (GCD) are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. We can use the following formula to find the LCM:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where 'a' and 'b' are the two numbers.
First, let's find the GCD of 8 and 10. The factors of 8 are 1, 2, 4, and 8. The factors of 10 are 1, 2, 5, and 10. The greatest common factor is 2. Therefore, GCD(8, 10) = 2.
Now, let's apply the formula:
LCM(8, 10) = (8 x 10) / 2 = 80 / 2 = 40
Thus, the LCM of 8 and 10 is 40 using the GCD method.
Real-World Applications of LCM
The concept of LCM isn't just a theoretical exercise; it has many practical applications in various fields:
-
Scheduling: Imagine you have two events that occur at different intervals. One event happens every 8 days, and another every 10 days. To find out when both events will happen on the same day, you need to find the LCM of 8 and 10. The answer, 40, means both events will coincide every 40 days.
-
Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial to find a common denominator, simplifying the calculation.
-
Music: In music theory, the LCM is used to determine the least common multiple of the note durations, helping in understanding rhythmic patterns and musical composition.
-
Construction and Engineering: In tasks involving repetitive processes with different cycle lengths, the LCM is vital for efficient scheduling and resource allocation.
-
Manufacturing: Production lines with different machine cycles often require the use of LCM to synchronize operations and optimize production flow.
Expanding on LCM Concepts
While we've focused on finding the LCM of two numbers, the concept extends to finding the LCM of three or more numbers. The methods remain similar, although the calculations become slightly more involved, especially with the prime factorization method. For multiple numbers, you would find the prime factorization of each number, then take the highest power of each distinct prime factor present in any of the factorizations and multiply them together.
For example, to find the LCM of 8, 10, and 12:
- Prime factorization of 8: 2³
- Prime factorization of 10: 2 x 5
- Prime factorization of 12: 2² x 3
The distinct prime factors are 2, 3, and 5. The highest powers are 2³, 3¹, and 5¹. Therefore, LCM(8, 10, 12) = 2³ x 3 x 5 = 8 x 3 x 5 = 120
Conclusion: Mastering LCM for Mathematical Success
Understanding the least common multiple is essential for a strong foundation in mathematics. Whether you're a student tackling fractions or a professional engineer optimizing production lines, the ability to efficiently calculate the LCM is a valuable skill. This article has explored three methods for finding the LCM, emphasizing the prime factorization method for its efficiency, especially with larger numbers. By grasping these concepts and their applications, you can confidently tackle more complex mathematical problems and expand your problem-solving capabilities. Remember to practice regularly to solidify your understanding and improve your speed and accuracy. The more you practice, the easier it will become to identify and apply the most appropriate method for any given problem. Mastering the LCM is a stepping stone towards greater mathematical fluency and success in various fields.
Latest Posts
Latest Posts
-
Oz In A Cup Of Butter
Apr 04, 2025
-
8 3 As A Mixed Number
Apr 04, 2025
-
What Type Of Symmetry Do Sponges Have
Apr 04, 2025
-
Oz In A Liter Of Water
Apr 04, 2025
-
How Far Is Venus From Sun
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm For 8 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
