What Is The Lcm Of 2 And 3
Kalali
Apr 06, 2025 · 4 min read
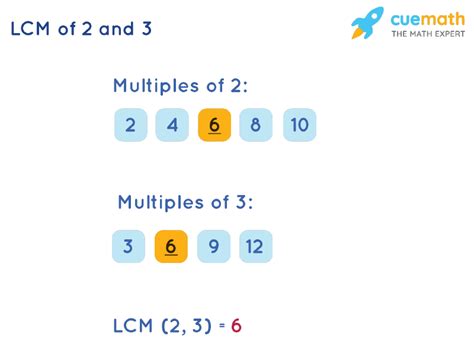
Table of Contents
What is the LCM of 2 and 3? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly in arithmetic and number theory. Understanding LCMs is crucial for various applications, from simplifying fractions to solving problems involving cycles and periodic events. This comprehensive guide will explore the LCM of 2 and 3, providing a detailed explanation of the concept, different methods for calculating LCMs, and practical examples. We'll also delve into the broader context of LCMs and their relevance in more advanced mathematical concepts.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the given numbers as factors. For example, the LCM of 4 and 6 is 12 because 12 is the smallest number that is divisible by both 4 and 6.
Key Differences between LCM and GCD:
Often confused with the greatest common divisor (GCD), the LCM represents the smallest common multiple, while the GCD represents the largest common factor. While seemingly opposites, the LCM and GCD are closely related, and knowing one can help you find the other. We'll explore this relationship later.
Calculating the LCM of 2 and 3: Different Methods
There are several ways to calculate the LCM of 2 and 3. Let's explore the most common methods:
Method 1: Listing Multiples
The simplest method is to list the multiples of each number until you find the smallest common multiple.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, ...
- Multiples of 3: 3, 6, 9, 12, 15, 18, ...
By comparing the lists, we see that the smallest common multiple is 6. Therefore, the LCM(2, 3) = 6.
Method 2: Prime Factorization
Prime factorization is a more efficient method for larger numbers. It involves breaking down each number into its prime factors.
- Prime factorization of 2: 2 (2 is a prime number)
- Prime factorization of 3: 3 (3 is a prime number)
To find the LCM using prime factorization, we take the highest power of each prime factor present in the numbers and multiply them together. In this case:
LCM(2, 3) = 2 × 3 = 6
Method 3: Using the Formula (LCM and GCD Relationship)
The LCM and GCD of two numbers are related by the following formula:
LCM(a, b) × GCD(a, b) = a × b
Where 'a' and 'b' are the two numbers.
First, let's find the GCD(2, 3). The greatest common divisor of 2 and 3 is 1 (as they share no common factors other than 1).
Now, applying the formula:
LCM(2, 3) × GCD(2, 3) = 2 × 3 LCM(2, 3) × 1 = 6 LCM(2, 3) = 6
Applications of LCM
The concept of LCM extends far beyond simple arithmetic exercises. It finds practical applications in various fields:
1. Fraction Addition and Subtraction:
Finding a common denominator when adding or subtracting fractions involves calculating the LCM of the denominators. For instance, to add 1/2 and 1/3, we need to find the LCM of 2 and 3, which is 6. We then rewrite the fractions with the common denominator:
1/2 + 1/3 = (3/6) + (2/6) = 5/6
2. Scheduling and Cyclical Events:
LCMs are essential for scheduling events that occur at regular intervals. For example, if bus A arrives every 2 hours and bus B arrives every 3 hours, the LCM of 2 and 3 (which is 6) tells us that both buses will arrive simultaneously every 6 hours.
3. Gear Ratios and Mechanical Systems:
In mechanical engineering, LCM is used in calculating gear ratios and determining the synchronized rotation of different gears in a system.
Advanced Concepts and Extensions
The concept of LCM can be extended to more than two numbers. For example, to find the LCM of 2, 3, and 4, we can use prime factorization:
- 2 = 2
- 3 = 3
- 4 = 2²
The LCM(2, 3, 4) = 2² × 3 = 12
Conclusion: The Significance of LCM(2,3) = 6
The seemingly simple calculation of the LCM of 2 and 3, which equals 6, serves as a fundamental building block for understanding and applying the concept of least common multiples. Its practical applications span various fields, highlighting its importance in both basic arithmetic and more advanced mathematical and engineering contexts. Mastering the concept of LCM is crucial for anyone seeking a deeper understanding of number theory and its practical implications. This comprehensive guide has provided various methods to calculate LCM and highlighted the importance of understanding this fundamental mathematical concept. Remember to practice these different methods to solidify your understanding and become proficient in calculating LCMs for a wider range of numbers.
Latest Posts
Latest Posts
-
What Is 7 Out Of 9 As A Percentage
Apr 08, 2025
-
What Is 15 16 As A Decimal
Apr 08, 2025
-
What Is Thirty Percent Of One Hundred
Apr 08, 2025
-
How Much Is 23 Cm In Inches
Apr 08, 2025
-
100 Cm In Inches And Feet
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 2 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.