What Is The Lcm Of 3 And 8
Kalali
Apr 01, 2025 · 4 min read
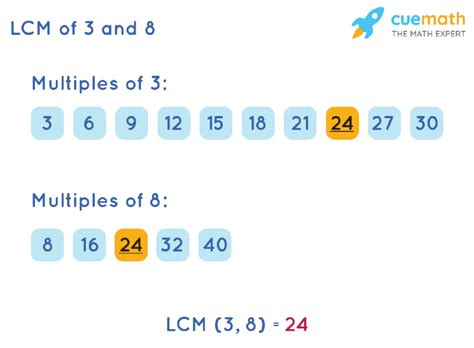
Table of Contents
What is the LCM of 3 and 8? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly in arithmetic and number theory. It plays a crucial role in various applications, from simplifying fractions to solving problems involving cycles and repetitions. This article delves deep into the question: What is the LCM of 3 and 8? We will explore multiple methods to find the answer, explain the underlying concepts, and expand on the broader significance of LCMs.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 3 and 8, let's solidify our understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
Consider two integers, 'a' and 'b'. Their LCM is denoted as LCM(a, b). For example:
- LCM(2, 3) = 6: 6 is the smallest number divisible by both 2 and 3.
- LCM(4, 6) = 12: 12 is the smallest number divisible by both 4 and 6.
- LCM(5, 10) = 10: 10 is the smallest number divisible by both 5 and 10.
Methods for Finding the LCM
Several methods exist for calculating the LCM of two or more integers. We'll explore the most common and effective approaches, applying them to find the LCM of 3 and 8.
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30... Multiples of 8: 8, 16, 24, 32, 40, 48...
The smallest multiple that appears in both lists is 24. Therefore, LCM(3, 8) = 24.
This method is simple but becomes less efficient with larger numbers. Imagine trying to find the LCM of 157 and 238 using this method!
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves expressing each number as a product of its prime factors.
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 8: 2 x 2 x 2 = 2³
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
Multiply these highest powers together: 2³ x 3 = 8 x 3 = 24
Therefore, LCM(3, 8) = 24 using the prime factorization method. This method is generally preferred for its efficiency and mathematical elegance.
3. Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
First, we find the GCD of 3 and 8. Since 3 is a prime number and 8 is not divisible by 3, their GCD is 1.
Now, we can use the formula:
LCM(3, 8) x GCD(3, 8) = 3 x 8 LCM(3, 8) x 1 = 24 LCM(3, 8) = 24
This method requires calculating the GCD first, which can be done using the Euclidean algorithm or prime factorization. However, it provides a valuable connection between LCM and GCD.
Applications of LCM
Understanding and calculating LCMs is crucial in various mathematical and real-world applications:
- Fraction addition and subtraction: Finding a common denominator for fractions involves finding the LCM of the denominators.
- Scheduling problems: Determining when events with different periodicities will occur simultaneously (e.g., buses arriving at a stop).
- Gear ratios: Calculating the least common multiple of gear teeth numbers for synchronized rotation.
- Cyclic processes: Analyzing repeating patterns or cycles in various systems.
- Music theory: Determining the least common multiple of note durations.
Expanding on the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, we consider all prime factors and their highest powers across all numbers. For the listing multiples method, it becomes considerably more tedious. The GCD method can also be adapted, but it requires more complex calculations.
For example, to find the LCM(3, 8, 6), we can use the prime factorization method:
- 3 = 3¹
- 8 = 2³
- 6 = 2¹ x 3¹
The highest power of 2 is 2³ = 8 The highest power of 3 is 3¹ = 3
LCM(3, 8, 6) = 2³ x 3 = 8 x 3 = 24
Conclusion: The Significance of LCM(3,8) = 24
We've definitively established that the LCM of 3 and 8 is 24. We've explored multiple methods to reach this conclusion, highlighting their strengths and weaknesses. Understanding how to calculate the LCM is essential for various mathematical and practical applications. The seemingly simple problem of finding the LCM of 3 and 8 serves as a gateway to understanding broader mathematical concepts and their real-world implications. The ability to efficiently and accurately determine LCMs is a valuable skill for students and professionals alike. This understanding forms the foundation for tackling more complex problems involving multiples and divisors. Mastering this concept lays the groundwork for more advanced mathematical explorations.
Latest Posts
Latest Posts
-
How Many Grams Is 1 2 Ounces
Apr 02, 2025
-
Cuantos Son 40 Grados Fahrenheit En Centigrados
Apr 02, 2025
-
Differentiate Between Extrusive And Intrusive Rocks
Apr 02, 2025
-
How Do You Write A Congruence Statement
Apr 02, 2025
-
What Is The Relationship Between Electron Affinity And Atomic Radius
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 3 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
