What Is The Lcm Of 8 And 9
Kalali
Apr 05, 2025 · 5 min read
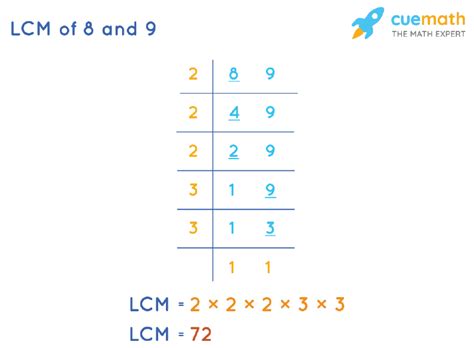
Table of Contents
What is the LCM of 8 and 9? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers is a fundamental concept in mathematics, with applications ranging from simple fraction addition to complex scheduling problems. This article will explore how to find the LCM of 8 and 9, providing a comprehensive understanding of the process and its underlying principles. We'll delve into various methods, from prime factorization to the listing method, illustrating each with clear examples and explanations. We'll also explore the broader context of LCMs and their significance in different mathematical fields.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 8 and 9, let's establish a solid foundation. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the numbers as factors.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... and multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Prime Factorization
This is arguably the most efficient and widely used method for finding the LCM of larger numbers. It involves breaking down each number into its prime factors. Prime factors are numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Steps:
-
Find the prime factorization of each number:
- 8 = 2 x 2 x 2 = 2³
- 9 = 3 x 3 = 3²
-
Identify the highest power of each prime factor present in the factorizations:
- The prime factors are 2 and 3.
- The highest power of 2 is 2³ = 8.
- The highest power of 3 is 3² = 9.
-
Multiply the highest powers together:
- LCM(8, 9) = 2³ x 3² = 8 x 9 = 72
Therefore, the LCM of 8 and 9 is 72.
Method 2: Listing Multiples
This method is straightforward but can become cumbersome with larger numbers. It involves listing the multiples of each number until a common multiple is found.
Steps:
-
List the multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80...
-
List the multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81...
The smallest multiple that appears in both lists is 72. Therefore, the LCM of 8 and 9 is 72.
Method 3: Using the Formula (For Two Numbers)
There's a convenient formula for calculating the LCM of two numbers using their greatest common divisor (GCD). The formula is:
LCM(a, b) = (a x b) / GCD(a, b)
where 'a' and 'b' are the two numbers.
Steps:
-
Find the GCD of 8 and 9:
The GCD of 8 and 9 is 1, as they share no common factors other than 1.
-
Apply the formula:
LCM(8, 9) = (8 x 9) / 1 = 72
Therefore, the LCM of 8 and 9 is 72.
Why is Understanding LCM Important?
The concept of LCM extends far beyond simple mathematical exercises. It has practical applications in various fields:
1. Fraction Addition and Subtraction:
Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For instance, to add 1/8 and 1/9, you'd need to find the LCM of 8 and 9 (which is 72), convert the fractions to equivalent fractions with a denominator of 72, and then add them.
2. Scheduling and Cyclical Events:
Imagine two buses that depart from the same stop, one every 8 minutes and the other every 9 minutes. The LCM helps determine when both buses will depart simultaneously again. In this case, the LCM(8, 9) = 72, meaning they'll depart together again in 72 minutes.
3. Modular Arithmetic and Cryptography:
LCM plays a crucial role in modular arithmetic, a branch of number theory used extensively in cryptography. Concepts like the Chinese Remainder Theorem, vital for secure communication protocols, rely heavily on understanding LCMs.
4. Music Theory:
In music theory, understanding LCMs is helpful for determining when different musical phrases or rhythms will coincide.
5. Construction and Engineering:
In construction, LCMs can assist in determining the optimal length of materials when dealing with repetitive patterns or structures.
Beyond Two Numbers: Finding the LCM of More Than Two Numbers
The prime factorization method readily extends to finding the LCM of more than two numbers. Simply find the prime factorization of each number, identify the highest power of each prime factor present, and then multiply these highest powers together.
For example, to find the LCM of 8, 9, and 12:
-
Prime factorizations:
- 8 = 2³
- 9 = 3²
- 12 = 2² x 3
-
Highest powers:
- Highest power of 2 is 2³ = 8
- Highest power of 3 is 3² = 9
-
Multiply:
- LCM(8, 9, 12) = 2³ x 3² = 8 x 9 = 72
Conclusion: The Power of the LCM
Understanding the LCM is essential for various mathematical and practical applications. While the listing method is conceptually simple, the prime factorization method provides a significantly more efficient approach, especially when dealing with larger numbers or multiple numbers simultaneously. Mastering LCM calculations opens doors to a deeper appreciation of number theory and its widespread relevance in the real world. The simple problem of finding the LCM of 8 and 9 serves as a gateway to understanding a fundamental concept with far-reaching implications. Remember that consistent practice and understanding the underlying principles will solidify your grasp of this important mathematical concept.
Latest Posts
Latest Posts
-
156 Cm To Inches And Feet
Apr 06, 2025
-
What Percent Is 10 Of 40
Apr 06, 2025
-
Atoms From Which Two Elements Would Form Ionic Bonds
Apr 06, 2025
-
60 Ounces Is How Many Cups
Apr 06, 2025
-
Cuanto Es El 30 Por Ciento De 300
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 8 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
