What Is The Least Common Factor Of 8 And 10
Kalali
Apr 02, 2025 · 5 min read
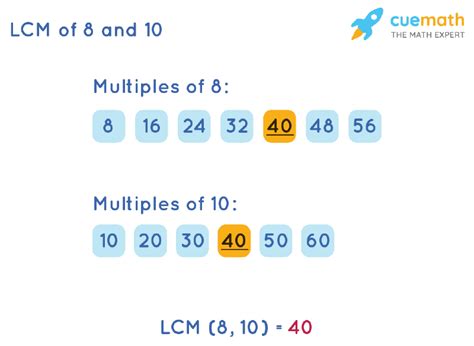
Table of Contents
- What Is The Least Common Factor Of 8 And 10
- Table of Contents
- What is the Least Common Factor of 8 and 10? A Deep Dive into Number Theory
- Understanding Least Common Multiples (LCM)
- Method 1: Listing Multiples
- Method 2: Prime Factorization
- Method 3: Using the Formula (LCM and GCF Relationship)
- Real-World Applications of LCM
- Extending the Concept: LCM of More Than Two Numbers
- Conclusion: Beyond the Numbers
- Latest Posts
- Latest Posts
- Related Post
What is the Least Common Factor of 8 and 10? A Deep Dive into Number Theory
Finding the least common factor (LCF) might seem like a simple arithmetic problem, but understanding the underlying concepts unlocks a deeper appreciation of number theory and its applications in various fields. While the term "least common factor" isn't standard mathematical terminology (it's usually referred to as the least common multiple or LCM), this article will address the question focusing on the concept of finding the smallest number that is a multiple of both 8 and 10. We'll explore different methods to solve this, delve into the significance of prime factorization, and showcase the broader implications of LCM in real-world scenarios.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 8 and 10, let's establish a solid understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder.
Key Differences Between LCM and GCF (Greatest Common Factor):
- LCM: Finds the smallest number that is a multiple of all the given numbers.
- GCF: Finds the largest number that is a factor of all the given numbers.
These two concepts are interconnected and often used together in various mathematical problems.
Method 1: Listing Multiples
One of the simplest methods to find the LCM of 8 and 10 is by listing their multiples. Let's start by listing the multiples of each number:
Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 96, 104, 112, 120...
Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120...
By comparing the two lists, we can identify the smallest number that appears in both lists. In this case, the smallest common multiple of 8 and 10 is 40.
Method 2: Prime Factorization
This method provides a more systematic and efficient approach, particularly when dealing with larger numbers. Prime factorization involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Prime Factorization of 8:
8 = 2 x 2 x 2 = 2³
Prime Factorization of 10:
10 = 2 x 5
Finding the LCM using Prime Factors:
-
Identify the highest power of each prime factor present in the factorizations: We have a prime factor of 2 (with the highest power of 2³) and a prime factor of 5 (with a power of 1).
-
Multiply the highest powers together: 2³ x 5 = 8 x 5 = 40
Therefore, the LCM of 8 and 10 is 40. This method is particularly useful when dealing with more than two numbers or larger numbers, making it a more robust and scalable technique.
Method 3: Using the Formula (LCM and GCF Relationship)
There's a helpful formula that connects the LCM and GCF (Greatest Common Factor) of two numbers. The formula states:
(Number 1) x (Number 2) = LCM(Number 1, Number 2) x GCF(Number 1, Number 2)
To use this, we first need to find the GCF of 8 and 10.
Finding the GCF of 8 and 10:
The factors of 8 are 1, 2, 4, 8. The factors of 10 are 1, 2, 5, 10. The greatest common factor is 2.
Applying the Formula:
(8) x (10) = LCM(8, 10) x GCF(8, 10) 80 = LCM(8, 10) x 2 LCM(8, 10) = 80 / 2 = 40
Real-World Applications of LCM
The concept of the least common multiple isn't confined to the realm of abstract mathematics. It finds practical applications in various real-world scenarios:
-
Scheduling and Time Management: Imagine you have two machines that perform different tasks. One machine runs a cycle every 8 hours, and the other every 10 hours. To determine when both machines will complete their cycles simultaneously, you need to find the LCM (40 hours). This helps in efficient scheduling and resource allocation.
-
Fractions and Least Common Denominator (LCD): When adding or subtracting fractions, you need to find a common denominator. This common denominator is simply the LCM of the denominators of the fractions. Finding the LCM ensures that the calculations are simplified and accurate.
-
Construction and Engineering: In construction, LCM helps in synchronizing different stages of a project where different work cycles need to be coordinated. This ensures smooth project flow and avoids delays.
-
Music and Rhythm: The LCM plays a role in understanding musical rhythms and harmonies. Determining when different rhythmic patterns align requires finding their LCM.
-
Cyclic Processes: In various scientific and engineering applications, you frequently encounter cyclical processes with different periods. Finding the LCM helps to predict when these cycles will coincide.
Extending the Concept: LCM of More Than Two Numbers
The methods described earlier can be extended to find the LCM of more than two numbers. The prime factorization method is particularly efficient for this purpose. For instance, let's find the LCM of 8, 10, and 12:
Prime Factorization:
8 = 2³ 10 = 2 x 5 12 = 2² x 3
Finding the LCM:
- Identify the highest power of each prime factor: 2³, 3¹, 5¹
- Multiply the highest powers: 2³ x 3 x 5 = 8 x 3 x 5 = 120
Therefore, the LCM of 8, 10, and 12 is 120.
Conclusion: Beyond the Numbers
Finding the least common multiple of 8 and 10 (which is 40) may seem like a basic mathematical exercise. However, by exploring different methods and understanding the underlying concepts of prime factorization and the relationship between LCM and GCF, we've uncovered a powerful tool with significant implications in various fields. The ability to efficiently determine the LCM enhances problem-solving capabilities in areas ranging from scheduling and fractions to complex engineering applications. This understanding transcends simple arithmetic and emphasizes the interconnectedness and practical value of number theory in our world. The next time you encounter an LCM problem, remember the elegance and versatility of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
A Marshmallow Is Cut In Half Physical Or Chemical Change
Apr 04, 2025
-
An Injured Limb Should Be Kept Above Heart Level
Apr 04, 2025
-
How Many Ounces Is 1 Cup Of Butter
Apr 04, 2025
-
Does My Brain Know I Have Eyes
Apr 04, 2025
-
Common Multiples Of 4 And 14
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Factor Of 8 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
