What Is The Percent For 1 20
Kalali
Apr 13, 2025 · 4 min read
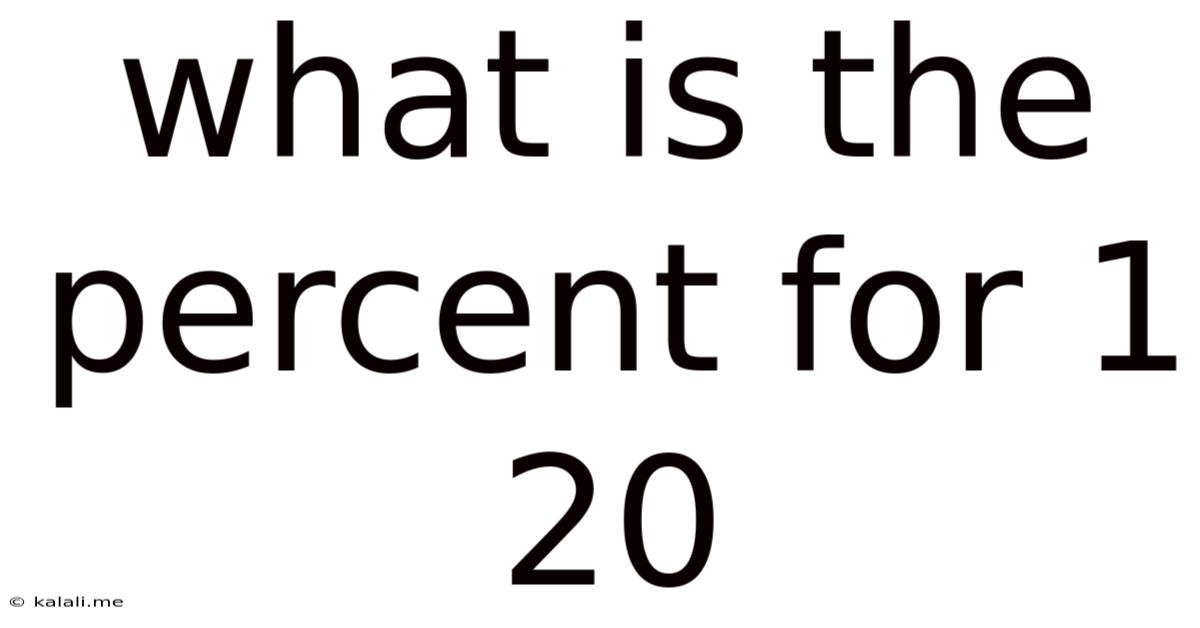
Table of Contents
What is the Percent for 1 of 20? Understanding Percentages and Their Applications
This article delves into the seemingly simple question: "What is the percent for 1 of 20?" While the answer might appear straightforward, understanding the underlying principles of percentage calculations is crucial for various applications in daily life, academics, and professional settings. We'll explore not just the calculation itself, but also the broader context of percentages, their uses, and how to apply this knowledge to more complex scenarios.
Meta Description: Learn how to calculate percentages with a detailed explanation of finding the percentage for 1 out of 20. This guide covers the basics, practical applications, and advanced percentage calculations.
Calculating the Percentage: 1 out of 20
To find the percentage representing 1 out of 20, we follow a simple formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 1 (the number we're interested in)
- Whole: 20 (the total number)
Therefore, the calculation is:
(1 / 20) * 100% = 5%
Thus, 1 out of 20 is 5%.
Understanding Percentages: A Deeper Dive
Percentages are a fundamental concept in mathematics and are used extensively to represent proportions or fractions as a portion of 100. They offer a standardized way to compare different quantities and express relative magnitudes. The percentage sign (%) signifies "per hundred" or "out of one hundred."
Key Concepts:
- Part: This represents the specific portion or quantity you are interested in expressing as a percentage.
- Whole: This represents the total quantity or the entire group from which the part is taken.
- Percentage: The numerical value expressing the proportion of the part to the whole, scaled to a base of 100.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable across numerous domains:
-
Finance: Calculating interest rates, discounts, tax rates, profit margins, and investment returns all rely heavily on percentage calculations. For example, understanding the percentage change in your investment portfolio helps in making informed financial decisions. A 10% increase in your investments is significantly different from a 10% decrease.
-
Science and Statistics: Percentages are vital in scientific research, statistical analysis, and data representation. Expressing experimental results, survey findings, or population demographics as percentages facilitates clear communication and interpretation. For instance, reporting that 75% of participants in a study showed improvement illustrates the results more effectively than stating that 75 out of 100 participants improved.
-
Everyday Life: Calculating tips in restaurants, determining sale discounts, understanding nutritional information on food labels, and even interpreting weather forecasts often involves percentage calculations. For example, a 20% off sale on a product helps you quickly determine the final price.
-
Education: Percentages are extensively used in grading systems, assessing student performance, and representing statistics related to academic achievement. A student scoring 85% on an exam indicates a strong understanding of the material.
-
Business and Marketing: Analyzing market share, conversion rates, customer satisfaction scores, and sales growth all involves extensive use of percentages. A marketing campaign showing a 5% increase in conversion rates indicates success.
Beyond the Basics: More Complex Percentage Calculations
While calculating 5% from 1 out of 20 is straightforward, many real-world scenarios involve more complex percentage problems:
1. Finding the Part when the Percentage and Whole are Known:
Let's say you have a 20% discount on a $100 item. To find the discount amount (the part):
- Percentage: 20%
- Whole: $100
Formula: (Percentage/100) * Whole = Part
(20/100) * $100 = $20
The discount is $20.
2. Finding the Whole when the Percentage and Part are Known:
Imagine you received a 10% commission on a sale, and your commission was $50. To find the total sale amount (the whole):
- Percentage: 10%
- Part: $50
Formula: Part / (Percentage/100) = Whole
$50 / (10/100) = $500
The total sale amount was $500.
3. Calculating Percentage Increase or Decrease:
Suppose your salary increased from $50,000 to $60,000. To calculate the percentage increase:
- Original Value: $50,000
- New Value: $60,000
Formula: [(New Value - Original Value) / Original Value] * 100%
[($60,000 - $50,000) / $50,000] * 100% = 20%
Your salary increased by 20%.
4. Dealing with Multiple Percentages:
Sometimes, you need to calculate successive percentages. For example, a 10% discount followed by a 5% additional discount on an item. These cannot be simply added together (15%). You must calculate each discount sequentially.
Advanced Percentage Concepts:
-
Compound Interest: This involves earning interest on both the principal amount and accumulated interest, leading to exponential growth over time.
-
Percentage Points: This refers to the arithmetic difference between two percentages. For instance, an increase from 10% to 15% is a 5 percentage point increase, not a 50% increase.
-
Weighted Averages: This is used when different parts of a whole have different weights or importance.
Conclusion: Mastering Percentages for Real-World Success
Understanding percentages is a foundational skill with far-reaching applications. While the simple calculation of 5% for 1 out of 20 provides a starting point, mastering different percentage calculations empowers you to tackle more complex problems in various aspects of life. From managing personal finances to analyzing data in professional settings, a solid grasp of percentages enhances decision-making, problem-solving, and overall comprehension of quantitative information. By practicing different percentage calculations and understanding their diverse applications, you can significantly improve your analytical skills and navigate the numerical world with greater confidence. Remember to practice regularly to reinforce your understanding and build proficiency in applying these essential mathematical concepts.
Latest Posts
Latest Posts
-
How Many Feet Is 240 In
Apr 14, 2025
-
What Is The Percent Of 17 20
Apr 14, 2025
-
What Percent Of 60 Is 6
Apr 14, 2025
-
20 Out Of 25 Is What Percent
Apr 14, 2025
-
How Many Mm In 16 Inches
Apr 14, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percent For 1 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.