What Is The Percentage Of 4/25
Kalali
Apr 08, 2025 · 5 min read
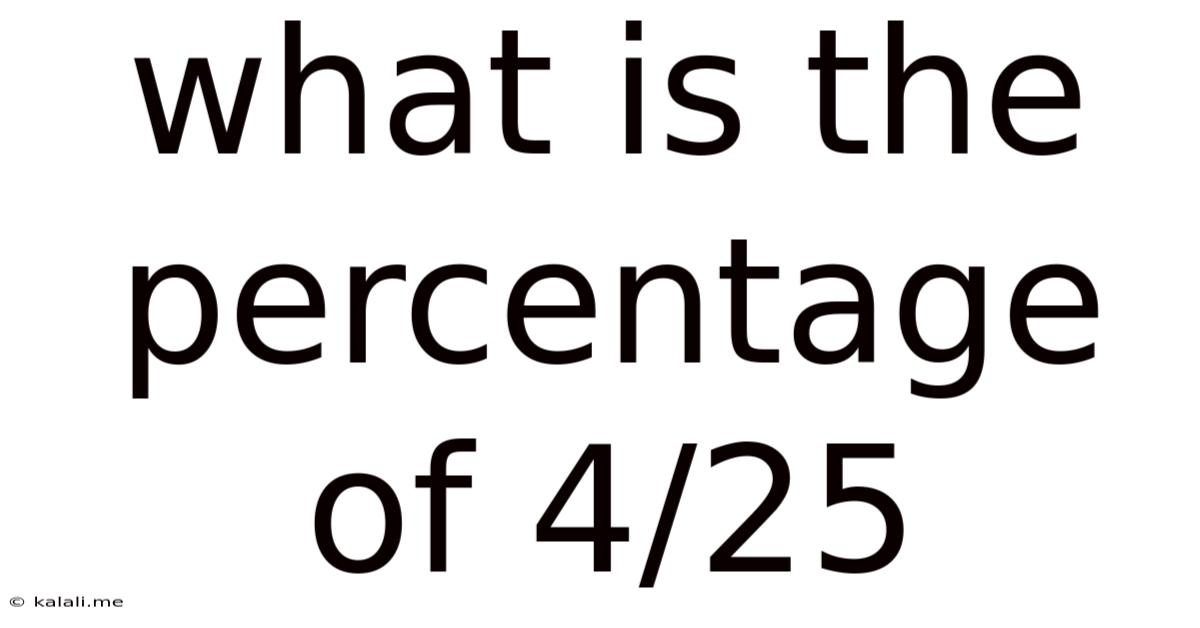
Table of Contents
What is the Percentage of 4/25? A Comprehensive Guide to Fractions, Decimals, and Percentages
This article delves deep into the seemingly simple question: what is the percentage of 4/25? While the answer itself is straightforward, understanding the underlying concepts of fractions, decimals, and percentages, and the methods for converting between them, is crucial for anyone seeking a solid grasp of basic mathematics and its applications. We'll cover multiple approaches to solving this problem, providing a comprehensive guide suitable for students, professionals, and anyone interested in enhancing their mathematical skills. This will include practical examples and explanations to solidify your understanding.
Meta Description: Learn how to convert the fraction 4/25 into a percentage. This comprehensive guide explains multiple methods, including the use of decimals, and provides practical examples for a thorough understanding.
Understanding Fractions, Decimals, and Percentages
Before diving into the calculation, let's establish a firm foundation in the three core concepts:
-
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of equal parts the whole is divided into. In our case, 4/25 means we have 4 parts out of a total of 25 equal parts.
-
Decimals: Decimals are another way to represent parts of a whole. They use a base-10 system, where each place value to the right of the decimal point represents a power of 10 (tenths, hundredths, thousandths, etc.). For example, 0.25 represents 2 tenths and 5 hundredths.
-
Percentages: Percentages express a fraction or decimal as a portion of 100. The percentage symbol (%) signifies "per hundred." For instance, 25% means 25 out of 100.
Method 1: Converting the Fraction to a Decimal, then to a Percentage
This is arguably the most common and straightforward method. We'll break it down step-by-step:
-
Divide the numerator by the denominator: To convert the fraction 4/25 to a decimal, we simply divide 4 by 25. This gives us 0.16.
-
Multiply the decimal by 100: To convert the decimal to a percentage, we multiply the decimal value (0.16) by 100. This results in 16.
-
Add the percentage symbol: Finally, add the percentage symbol (%) to indicate that the value represents a percentage.
Therefore, 4/25 is equal to 16%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method leverages the fact that percentages are based on 100. We can convert the fraction 4/25 to an equivalent fraction with a denominator of 100, making the conversion to a percentage much simpler.
-
Determine the factor: We need to determine what number we need to multiply the denominator (25) by to get 100. In this case, 25 x 4 = 100.
-
Multiply both the numerator and denominator: To maintain the same value of the fraction, we must multiply both the numerator and denominator by the same factor (4). So, we have (4 x 4) / (25 x 4) = 16/100.
-
Convert to a percentage: Since the denominator is now 100, the numerator directly represents the percentage. Therefore, 16/100 is equal to 16%.
Method 3: Using Proportions
Proportions offer a more formal mathematical approach to solving this problem. We can set up a proportion to find the equivalent percentage:
4/25 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
25x = 400
Then, divide both sides by 25:
x = 400/25 = 16
Therefore, x = 16%.
Real-World Applications of Percentage Calculations
Understanding how to calculate percentages isn't just an academic exercise; it has numerous practical applications in everyday life and various professional fields. Here are a few examples:
-
Calculating discounts: If a store offers a 20% discount on an item, you can easily calculate the discount amount and the final price by converting the percentage to a decimal and performing the necessary calculations.
-
Determining tax amounts: Sales tax is often expressed as a percentage. Knowing how to calculate percentages allows you to determine the exact tax amount you'll need to pay.
-
Analyzing financial statements: Financial statements, such as income statements and balance sheets, often present data as percentages. Understanding these percentages is crucial for making informed financial decisions.
-
Understanding statistical data: Percentages are frequently used to represent statistical data, such as market share, survey results, and economic indicators. Being able to interpret these percentages is essential for comprehending the data.
-
Calculating interest rates: Interest rates on loans and investments are often expressed as percentages. Understanding how to calculate percentages is essential for making informed decisions about borrowing and investing.
-
Grading systems: Many educational institutions use percentages to represent grades. Understanding how percentages are calculated helps students track their academic progress.
Advanced Concepts and Further Exploration
While this article focuses on the fundamental methods for calculating the percentage of 4/25, several advanced concepts build upon this foundation:
-
Compound interest: This involves calculating interest on both the principal amount and accumulated interest from previous periods.
-
Percentage change: This measures the relative change in a value over time, expressed as a percentage.
-
Percentage points: This represents the absolute difference between two percentages, rather than a relative change.
Conclusion
Calculating the percentage of 4/25, resulting in 16%, is a relatively simple task, but the underlying concepts of fractions, decimals, and percentages are fundamental to numerous mathematical applications. Understanding these concepts and the various methods for converting between them provides a robust foundation for tackling more complex mathematical problems in various real-world scenarios. By mastering these techniques, you'll equip yourself with essential skills for navigating everyday life and professional endeavors. Remember to practice regularly to solidify your understanding and build confidence in your mathematical abilities. The more you practice, the easier and more intuitive these calculations will become.
Latest Posts
Latest Posts
-
Cuanto Son 66 Grados Fahrenheit En Centigrados
Apr 17, 2025
-
2 Is What Percent Of 6
Apr 17, 2025
-
Food Chain In The Rainforest Tropical
Apr 17, 2025
-
How Many Oz For 1 Pound
Apr 17, 2025
-
Cuanto Es 2 Metros En Pulgadas
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 4/25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.