What Is The Percentage Of 6 Out Of 8
Kalali
Apr 06, 2025 · 5 min read
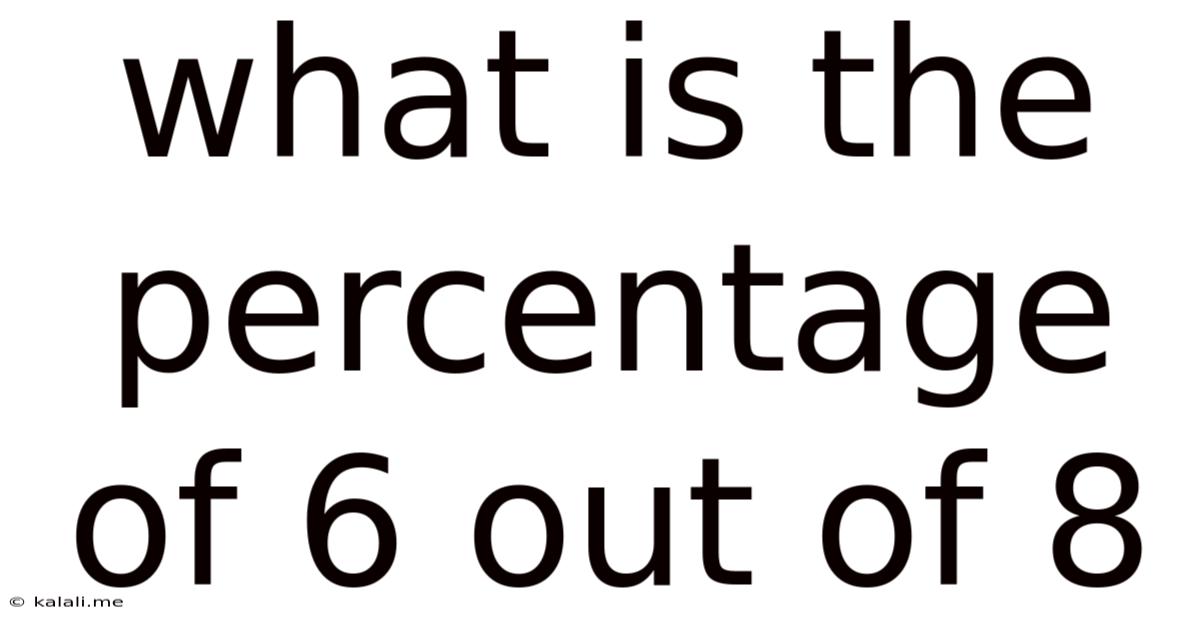
Table of Contents
What is the Percentage of 6 out of 8? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous fields, from finance and statistics to everyday life. This comprehensive guide will not only answer the question, "What is the percentage of 6 out of 8?" but also delve deep into the underlying principles of percentage calculations, providing you with the knowledge to tackle similar problems independently. We'll explore various methods, offer practical examples, and touch upon the broader applications of percentage calculations.
Understanding Percentages: The Basics
A percentage represents a fraction of 100. It indicates a proportion relative to a whole. The symbol "%" signifies "per cent," meaning "out of one hundred." So, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Key Terminology:
- Numerator: The top number in a fraction (in this case, 6). This represents the part.
- Denominator: The bottom number in a fraction (in this case, 8). This represents the whole.
- Percentage: The proportion expressed as a number out of 100.
Calculating the Percentage of 6 out of 8: The Step-by-Step Method
To find the percentage of 6 out of 8, we follow a straightforward three-step process:
Step 1: Formulate the Fraction:
Express the problem as a fraction: 6/8. This represents 6 parts out of a total of 8 parts.
Step 2: Convert the Fraction to a Decimal:
Divide the numerator (6) by the denominator (8): 6 ÷ 8 = 0.75
Step 3: Convert the Decimal to a Percentage:
Multiply the decimal by 100 and add the percentage symbol (%): 0.75 × 100 = 75%.
Therefore, 6 out of 8 is 75%.
Alternative Methods for Percentage Calculation
While the above method is the most common and straightforward, alternative approaches can offer different perspectives and are beneficial for understanding the underlying concepts.
Method 2: Using Proportions
We can set up a proportion to solve this:
6/8 = x/100
Where 'x' represents the percentage we want to find. Cross-multiplying, we get:
8x = 600
Dividing both sides by 8:
x = 75
Therefore, 6 out of 8 is 75%.
Method 3: Simplifying the Fraction First
Before converting to a decimal, we can simplify the fraction 6/8 by finding the greatest common divisor (GCD) of 6 and 8, which is 2. Dividing both the numerator and denominator by 2, we get:
6/8 = 3/4
Now, converting 3/4 to a decimal: 3 ÷ 4 = 0.75
Finally, converting the decimal to a percentage: 0.75 × 100 = 75%
This method demonstrates that simplifying the fraction can sometimes make the calculation easier.
Real-World Applications of Percentage Calculations
Understanding percentages is crucial in various aspects of daily life:
1. Finance and Budgeting:
- Interest rates: Banks and financial institutions use percentages to express interest rates on loans and savings accounts.
- Discounts and sales: Stores use percentages to advertise discounts on products. Calculating the actual price after a discount requires understanding percentage reductions.
- Taxes: Sales tax, income tax, and other taxes are often expressed as percentages.
- Investment returns: Investment performance is frequently expressed as a percentage return on investment.
2. Statistics and Data Analysis:
- Data representation: Percentages are commonly used to represent proportions within datasets, such as survey results or demographic information.
- Probability: Percentages are used to express probabilities, representing the likelihood of an event occurring.
- Statistical significance: In statistical analysis, percentages are used to assess the significance of findings.
3. Everyday Life:
- Tip calculations: Calculating a tip in a restaurant involves determining a percentage of the bill.
- Grading systems: Many educational systems use percentages to represent grades and scores.
- Recipe scaling: Adjusting recipes to serve a larger or smaller number of people often involves percentage calculations.
- Comparing quantities: Percentages make it easy to compare proportions between different quantities.
Advanced Percentage Calculations: Going Beyond the Basics
While the example of 6 out of 8 is relatively simple, understanding percentages extends to more complex scenarios.
1. Calculating Percentage Increase or Decrease:
These calculations are essential for tracking changes over time. For example, if a quantity increases from 50 to 60, the percentage increase is calculated as:
[(60 - 50) / 50] × 100 = 20%
Similarly, a decrease from 60 to 50 represents a 16.67% decrease.
2. Finding the Original Value after a Percentage Change:
If a value has been increased or decreased by a certain percentage, and you know the final value, you can work backward to find the original value. For example, if a price increased by 10% to reach $110, the original price was $100. This calculation requires understanding reverse percentage calculations.
3. Calculating Percentage Points:
It's crucial to distinguish between percentage points and percentage change. A change from 20% to 30% is a 10 percentage point increase, not a 50% increase. Percentage points represent the absolute difference between two percentages.
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The more you practice, the more comfortable you'll become with these calculations.
- Use Different Methods: Experiment with various approaches to reinforce your understanding.
- Understand the Concepts: Focus on understanding the underlying principles rather than just memorizing formulas.
- Check Your Answers: Always double-check your calculations to ensure accuracy.
- Utilize Online Calculators (Sparingly): While online calculators can be helpful, they shouldn't replace the understanding of the underlying methods. Use them for verification, not as a crutch.
Conclusion
Calculating the percentage of 6 out of 8, as we've demonstrated, is a straightforward process. However, the broader application of percentage calculations extends far beyond this single example. Mastering percentages is a valuable skill that will serve you well in various academic, professional, and personal settings. By understanding the fundamental principles and practicing different calculation methods, you can confidently tackle a wide array of percentage-related problems, enhancing your analytical abilities and problem-solving skills. Remember to focus on the concepts and apply your newfound knowledge to real-world situations to solidify your understanding.
Latest Posts
Latest Posts
-
Whats 1 Percent Of 1 Million
Apr 07, 2025
-
Who And When Was Carbon Discovered
Apr 07, 2025
-
A Substance That Combines With Hydrogen Ions
Apr 07, 2025
-
How Many Inches In 71 Cm
Apr 07, 2025
-
How Many Feet Are In 126 Inches
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 6 Out Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.