What Is The Range Of The Function Graphed Below
Kalali
Mar 28, 2025 · 6 min read
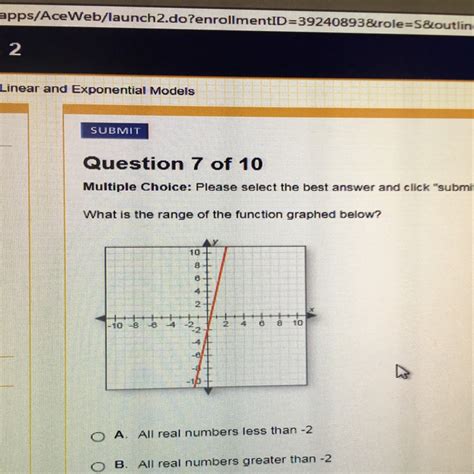
Table of Contents
Decoding the Range: A Comprehensive Guide to Understanding Function Ranges from Graphs
Determining the range of a function from its graph is a fundamental concept in mathematics. Understanding the range allows you to fully grasp the function's behavior and its limitations. This comprehensive guide will walk you through various methods to identify the range, covering different types of functions and complexities. We'll explore both visual inspection and analytical techniques, empowering you to confidently determine the range of any function presented graphically.
What is the Range of a Function?
Before diving into specific examples, let's establish a clear understanding of what constitutes a function's range. The range of a function is the complete set of all possible output values (y-values) that the function can produce. Think of it as the vertical extent of the function's graph – the span of y-values covered by the function. It's crucial to distinguish the range from the domain, which represents the set of all possible input values (x-values).
Methods for Determining the Range from a Graph
Several methods can be effectively employed to determine the range of a function from its graph:
1. Visual Inspection:
This is the most straightforward approach, especially for functions with simple graphs. Carefully examine the graph and observe the lowest and highest y-values the graph attains. Consider:
-
Continuous Functions: For continuous functions (functions without any breaks or jumps), the range typically includes all y-values between the minimum and maximum y-values.
-
Discontinuous Functions: For discontinuous functions (functions with breaks or jumps), the range might exclude certain y-values. Carefully note any gaps or asymptotes (lines the graph approaches but never touches).
-
Bounded vs. Unbounded Functions: If the graph extends infinitely upwards or downwards, the range will be unbounded (e.g., (−∞, ∞)). If the graph remains within a specific vertical boundary, the range will be bounded.
Example: Consider a simple parabola opening upwards. Visually inspecting its graph reveals a minimum y-value (the vertex) and an upward extension towards infinity. The range, therefore, would be represented as [minimum y-value, ∞).
2. Identifying Key Features:
Certain graphical features are essential for accurately determining the range:
-
Vertex of a Parabola: For parabolas, the y-coordinate of the vertex provides the minimum or maximum value of the function, determining the lower or upper bound of the range.
-
Asymptotes: Asymptotes, whether horizontal or oblique, often indicate limitations in the range. The function approaches but never reaches the asymptote's y-value.
-
Intercepts: While not always directly determining range boundaries, y-intercepts (where the graph intersects the y-axis) can provide valuable information about the range's inclusion of specific y-values.
3. Analytical Approach (using the function's equation):
When the function's equation is known, an analytical approach might be more accurate and precise than mere visual inspection. This involves determining the function's behavior by examining its equation:
-
Finding Critical Points: Determine the critical points (maxima, minima, and inflection points) using calculus techniques (finding derivatives and setting them to zero). These points provide insights into the function's extreme values, impacting range boundaries.
-
Analyzing the Function's Behavior: Examine the function's equation to understand its behavior as x approaches positive and negative infinity. This reveals whether the range is bounded or unbounded.
-
Transformations: If the function is a transformation of a known function (e.g., a shifted or scaled parabola), use your knowledge of transformations to deduce the range from the original function's range.
Examples Illustrating Range Determination
Let's delve into several examples showcasing diverse function types and range determination techniques:
Example 1: A simple linear function
Consider the function f(x) = 2x + 1. Its graph is a straight line. Since a linear function extends infinitely in both directions, its range is (-∞, ∞).
Example 2: A quadratic function
Let's analyze the function f(x) = x² - 4x + 5. This is a parabola. Completing the square, we get f(x) = (x - 2)² + 1. The vertex is at (2, 1), which represents the minimum value. Therefore, the range is [1, ∞).
Example 3: A piecewise function
Consider a piecewise function defined as: f(x) = x + 2, if x < 0 f(x) = x², if x ≥ 0
For x < 0, the function is a line extending from (-∞, 2). For x ≥ 0, it's a parabola starting at (0,0) and extending to infinity. Therefore, the range is (-∞, ∞).
Example 4: A rational function
Consider the function f(x) = 1/x. This function has a vertical asymptote at x = 0 and a horizontal asymptote at y = 0. The function never reaches y = 0. Therefore, the range is (-∞, 0) U (0, ∞).
Example 5: A trigonometric function (sine)
The sine function, f(x) = sin(x), oscillates between -1 and 1. Its range is [-1, 1].
Example 6: A function with a square root
The function f(x) = √(x-2) involves a square root, which means that the expression inside the square root must be greater than or equal to zero: x - 2 ≥ 0 which implies x ≥ 2. This sets a limit on the domain. The range, in this case, starts at y = 0 and extends to positive infinity. Thus, the range is [0, ∞).
Example 7: Absolute Value Function
Consider the function f(x) = |x| + 2. The absolute value function |x| is always non-negative (zero or positive). Adding 2 shifts the graph vertically up by two units. Therefore, the range is [2, ∞).
Example 8: A function with a hole
Consider a function with a removable discontinuity (hole) at, say, x=1. Even if the function is undefined at x=1, if the y-values on either side of x=1 approach the same limit, the range will include the limiting value. For example, if the graph approaches y=3 on both sides of x=1, the range will still include 3. However, if there is a jump discontinuity (a non-removable discontinuity), the range will exclude the value the function jumps over.
Advanced Considerations and Challenges
-
Implicit Functions: Determining the range of implicit functions (where the relationship between x and y is not explicitly stated as y = f(x)) can be more challenging. Graphical analysis often becomes the primary method.
-
Functions with Multiple Branches: Functions with multiple branches (defined differently over different intervals) require careful analysis of each branch separately to determine the overall range.
-
Using Technology: Graphing calculators and software can aid in visualizing the function's graph and estimating the range, especially for complex functions. However, always double-check the results using analytical methods to ensure accuracy.
Conclusion
Mastering the skill of determining the range of a function is crucial for a thorough understanding of function behavior. By combining visual inspection of the graph with analytical techniques, you can effectively tackle a wide range of functions, from simple linear equations to complex multi-branch functions. Remember to carefully examine key graphical features like vertices, asymptotes, and discontinuities to precisely define the range. While technology can assist in visualization, a solid grasp of the underlying mathematical concepts remains essential for confident and accurate range determination. The more practice you get, the more intuitively you will be able to determine the range of a function from its graph.
Latest Posts
Latest Posts
-
Chemical Change In Cooking An Egg
Mar 31, 2025
-
Is Grain Alcohol A Pure Substance Or Mixture
Mar 31, 2025
-
4 Right Angles And 2 Pairs Of Parallel Sides
Mar 31, 2025
-
What Do You Call Frogs Fingers
Mar 31, 2025
-
Cuanto Es 500 Gramos En Libras
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Range Of The Function Graphed Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
