What Number Is 20 Of 50
Kalali
Apr 25, 2025 · 5 min read
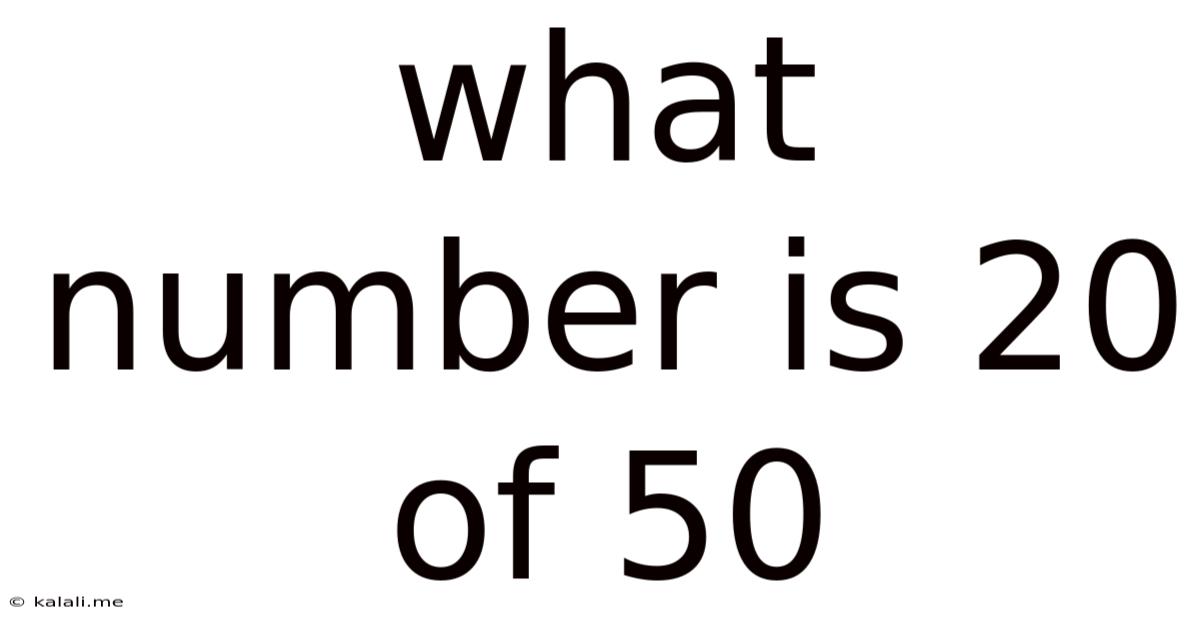
Table of Contents
What Number is 20 of 50? Deconstructing Percentages, Fractions, and Ratios
What number is 20 of 50? At first glance, this seems like a simple question with a straightforward answer. However, exploring this seemingly basic problem opens the door to understanding fundamental mathematical concepts like percentages, fractions, and ratios – all crucial for various applications in everyday life and advanced studies. This article will delve deep into this seemingly simple query, exploring different ways to solve it and highlighting the broader mathematical principles involved. This will equip you with a strong foundation in understanding proportional relationships and applying them in different contexts.
Meta Description: This comprehensive guide explores the question "What number is 20 of 50?" by examining percentages, fractions, and ratios. Learn multiple approaches to solving this problem and gain a solid understanding of proportional relationships.
Understanding the Core Concept: Proportions
Before diving into calculations, let's establish the core concept at play: proportions. A proportion is a statement that two ratios are equal. In simpler terms, it's a comparison of two quantities. Our problem, "What number is 20 of 50?", can be framed as a proportion problem: 20 is what percentage (or fraction) of 50?
We can represent this as:
20/50 = x/100 (where x represents the percentage)
or
20/50 = x/1 (where x represents the fraction)
These representations allow us to solve for x using different mathematical techniques.
Method 1: Using Percentages
Percentages provide a standardized way to express proportions. A percentage is a fraction where the denominator is 100. To find what percentage 20 is of 50, we can use the following formula:
(Part / Whole) * 100 = Percentage
In our case:
(20 / 50) * 100 = 40%
Therefore, 20 is 40% of 50. This method is straightforward and widely applicable in various real-world scenarios, such as calculating discounts, tax rates, and grades.
Method 2: Using Fractions
Fractions offer another way to represent proportions. A fraction expresses a part of a whole. In our problem, 20 is the part, and 50 is the whole. The fraction representing this relationship is:
20/50
This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 10:
20/50 = 2/5
Therefore, 20 is 2/5 of 50. This fractional representation is useful when dealing with proportions involving discrete quantities or when precise ratios are needed.
Method 3: Using Ratios
Ratios express the quantitative relationship between two or more quantities. In our case, the ratio of 20 to 50 is:
20:50
Similar to fractions, this ratio can be simplified by dividing both terms by their GCD (10):
20:50 = 2:5
The ratio 2:5 indicates that for every 2 units of one quantity, there are 5 units of another quantity. This representation is particularly useful when comparing different sets of quantities or when scaling up or down proportions.
Method 4: Cross-Multiplication (for Proportion Problems)
As mentioned earlier, we can express the problem as a proportion:
20/50 = x/100 (to find the percentage)
or
20/50 = x/1 (to find the equivalent fraction)
To solve for x using cross-multiplication, we multiply the numerator of one fraction by the denominator of the other and set them equal:
For Percentage:
20 * 100 = 50 * x
2000 = 50x
x = 2000 / 50
x = 40
Therefore, x = 40%, confirming our earlier calculation.
For Fraction:
20 * 1 = 50 * x
20 = 50x
x = 20 / 50
x = 2/5
This method reinforces the concept of equivalent ratios and demonstrates the power of algebraic manipulation in solving proportion problems.
Real-World Applications of Proportions
Understanding proportions is crucial in many aspects of life:
-
Cooking: Scaling recipes up or down requires understanding proportions. If a recipe calls for 2 cups of flour and 1 cup of sugar, you need to maintain the 2:1 ratio when making a larger or smaller batch.
-
Finance: Calculating interest, discounts, tax amounts, and profit margins all rely on proportional relationships.
-
Science: Many scientific principles and calculations are based on proportions, such as calculating concentrations, dilutions, and reaction rates.
-
Engineering: Designing structures, calculating loads, and scaling models all involve understanding proportions.
-
Data Analysis: Analyzing data often involves comparing different proportions to identify trends, patterns, and relationships.
-
Mapping and Scaling: Creating maps and scaling drawings accurately rely on precise proportional relationships.
Beyond the Basics: Advanced Proportion Concepts
While our initial problem was relatively simple, the underlying principles can be extended to more complex scenarios:
-
Compound Proportions: These involve multiple ratios interacting simultaneously. For instance, calculating the time it takes to complete a task when multiple workers are involved with different work rates.
-
Inverse Proportions: In some cases, an increase in one quantity results in a decrease in another, creating an inverse proportion. Speed and travel time are inversely proportional; the faster you go, the shorter the travel time.
-
Proportional Reasoning: This involves the ability to analyze and solve problems involving proportions, requiring a deep understanding of ratios, fractions, and percentages.
Conclusion: Mastering Proportions for Success
The seemingly simple question, "What number is 20 of 50?", serves as a gateway to understanding the powerful concept of proportions. By exploring different methods—percentages, fractions, ratios, and cross-multiplication—we've not only answered the initial question but also gained a deeper understanding of proportional relationships and their widespread applications. Mastering these concepts is crucial for success in various fields, from everyday tasks to advanced scientific and engineering endeavors. The ability to effectively utilize proportional reasoning is a valuable skill that enhances problem-solving capabilities and fosters a deeper comprehension of mathematical principles. This article aims to provide a comprehensive foundation for further exploration and application of these essential mathematical tools.
Latest Posts
Latest Posts
-
What Is 21 5 Cm In Inches
Apr 25, 2025
-
Angle Of Elevation And Depression Word Problems
Apr 25, 2025
-
How Much Is 2 1 2 Quarts
Apr 25, 2025
-
Which Alkali Metal Is Most Reactive
Apr 25, 2025
-
What Percent Of 72 Is 27
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about What Number Is 20 Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.