What Percent Is 10 Of 20
Kalali
Apr 18, 2025 · 6 min read
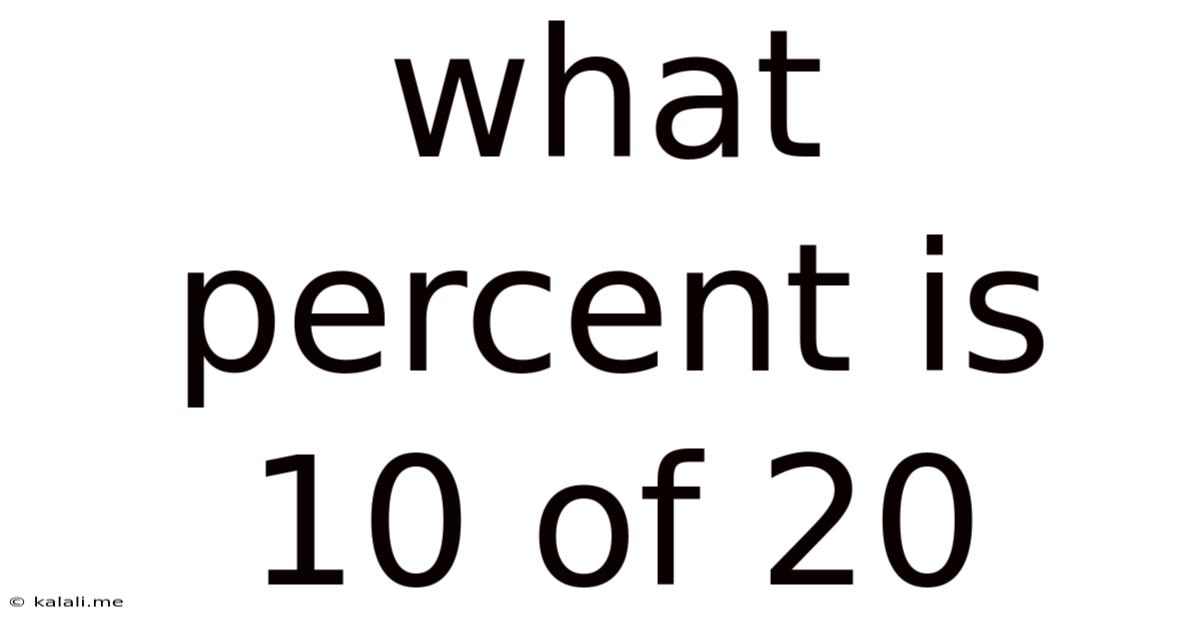
Table of Contents
What Percent is 10 of 20? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What percent is 10 of 20?", opens the door to a fascinating exploration of percentages, their calculation, and their widespread use in various fields. While the answer itself is straightforward – 50% – understanding the underlying concepts and applications provides a much richer understanding of this fundamental mathematical concept. This article will not only answer the question but delve into the mechanics of percentage calculation, explore different methods of solving similar problems, and showcase the practical applications of percentages in everyday life and various professions.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to determine what percent 10 is of 20. This guide covers various methods, real-world applications, and practical examples to master percentage calculations.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 50% literally means 50 out of 100, or 50/100, which simplifies to 1/2. This simple understanding is the cornerstone of all percentage calculations.
The fundamental formula for calculating percentages is:
(Part / Whole) * 100 = Percentage
In our example, "What percent is 10 of 20?", 10 is the part and 20 is the whole. Applying the formula:
(10 / 20) * 100 = 50%
Multiple Methods for Calculating Percentages
While the basic formula is straightforward, several methods can be used to calculate percentages, each offering its own advantages depending on the context and the complexity of the problem.
Method 1: The Basic Formula (as shown above)
This is the most fundamental and widely applicable method. It's easy to understand and use for simple percentage calculations. Its simplicity makes it suitable for both manual calculations and programming.
Method 2: Using Decimals
Percentages can be easily converted to decimals by dividing the percentage by 100. For instance, 50% is equal to 0.5. This method is particularly useful when working with calculators or spreadsheets. To find what percent 10 is of 20 using this method:
- Divide the part by the whole: 10 / 20 = 0.5
- Multiply by 100: 0.5 * 100 = 50%
Method 3: Cross-Multiplication
This method is helpful when dealing with more complex percentage problems. It involves setting up a proportion and solving for the unknown variable. For our example:
- Let x represent the percentage we're trying to find.
- We can set up the proportion: 10/20 = x/100
- Cross-multiply: 10 * 100 = 20 * x
- Solve for x: 1000 = 20x => x = 50
Therefore, 10 is 50% of 20.
Method 4: Using Proportions and Ratios
Understanding ratios and proportions provides a deeper insight into the relationships between numbers and percentages. In this case, the ratio of 10 to 20 is 1:2. To express this as a percentage, we need to find an equivalent ratio with a denominator of 100. This can be done by multiplying both parts of the ratio by 50:
(1 * 50) : (2 * 50) = 50 : 100 This directly translates to 50%.
Real-World Applications of Percentage Calculations
Percentages are ubiquitous, appearing in almost every aspect of our lives. Understanding percentage calculations is essential for navigating various situations effectively.
1. Finance and Budgeting:
- Interest rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. Understanding interest rates is crucial for making informed financial decisions.
- Taxes: Taxes are usually expressed as percentages of income or the value of goods and services. Calculating tax amounts requires a solid understanding of percentages.
- Discounts and Sales: Retailers frequently offer discounts expressed as percentages. Calculating the final price after a discount involves subtracting the percentage discount from the original price.
- Investment returns: Investment returns are often expressed as percentages, allowing investors to compare the performance of different investment options.
2. Science and Statistics:
- Data analysis: Percentages are frequently used to represent proportions and trends in data analysis. This is essential for interpreting research findings and making data-driven decisions.
- Probability: Probability is often expressed as a percentage, indicating the likelihood of an event occurring.
- Scientific measurements: Percentages are used to express concentrations, errors, and other quantitative aspects in scientific experiments and measurements.
3. Everyday Life:
- Tip calculations: Calculating tips in restaurants usually involves determining a certain percentage of the bill.
- Grade calculations: Academic grades often reflect a percentage of correct answers or total points earned.
- Recipe scaling: Adjusting recipes involves scaling ingredients up or down using percentages.
- Sales commissions: Sales representatives frequently earn commissions based on a percentage of their sales.
4. Business and Marketing:
- Market share: Companies track their market share using percentages to understand their position within a particular industry.
- Profit margins: Businesses calculate profit margins using percentages to determine their profitability.
- Growth rates: Companies analyze their growth rate using percentages to track progress over time.
- Conversion rates: In marketing and sales, conversion rates (e.g., from website visitors to customers) are crucial metrics, expressed as percentages.
Advanced Percentage Problems and Solutions
While "What percent is 10 of 20?" is a basic problem, understanding the concepts allows us to tackle more complex scenarios. Let's explore a few examples:
Example 1: If a shirt is discounted by 25% from its original price of $50, what is the final price?
- Calculate the discount amount: 25% of $50 = (25/100) * $50 = $12.50
- Subtract the discount from the original price: $50 - $12.50 = $37.50 Therefore, the final price of the shirt is $37.50.
Example 2: If a student scores 80 out of 100 on a test, what is their percentage score?
(80 / 100) * 100 = 80%
Example 3: A store increased its prices by 15%. If the original price of an item was $20, what is the new price?
- Calculate the price increase: 15% of $20 = (15/100) * $20 = $3
- Add the increase to the original price: $20 + $3 = $23 The new price of the item is $23.
Conclusion: Mastering Percentages for Success
The seemingly simple question, "What percent is 10 of 20?", serves as a gateway to a much broader understanding of percentages and their crucial role in various aspects of life. From managing personal finances to analyzing complex datasets, the ability to calculate and interpret percentages is an invaluable skill. Mastering the different methods of calculation, as outlined in this article, empowers individuals to confidently tackle diverse percentage problems and apply this knowledge to real-world situations, leading to more informed decisions and enhanced problem-solving capabilities. The fundamental principles discussed here form a robust foundation for tackling more advanced percentage-related challenges encountered in various fields. Remember, consistent practice and a thorough understanding of the underlying concepts are key to mastering the world of percentages.
Latest Posts
Latest Posts
-
3 Out Of 13 As A Percentage
Apr 19, 2025
-
Which Statement Describes An Atomic Nucleus
Apr 19, 2025
-
What Is A Factor Of 56
Apr 19, 2025
-
Least Common Multiple Of 9 And 10
Apr 19, 2025
-
500 Ml Is How Many Cups Of Water
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 10 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.