What Percent Is 21 Out Of 30
Kalali
Apr 11, 2025 · 5 min read
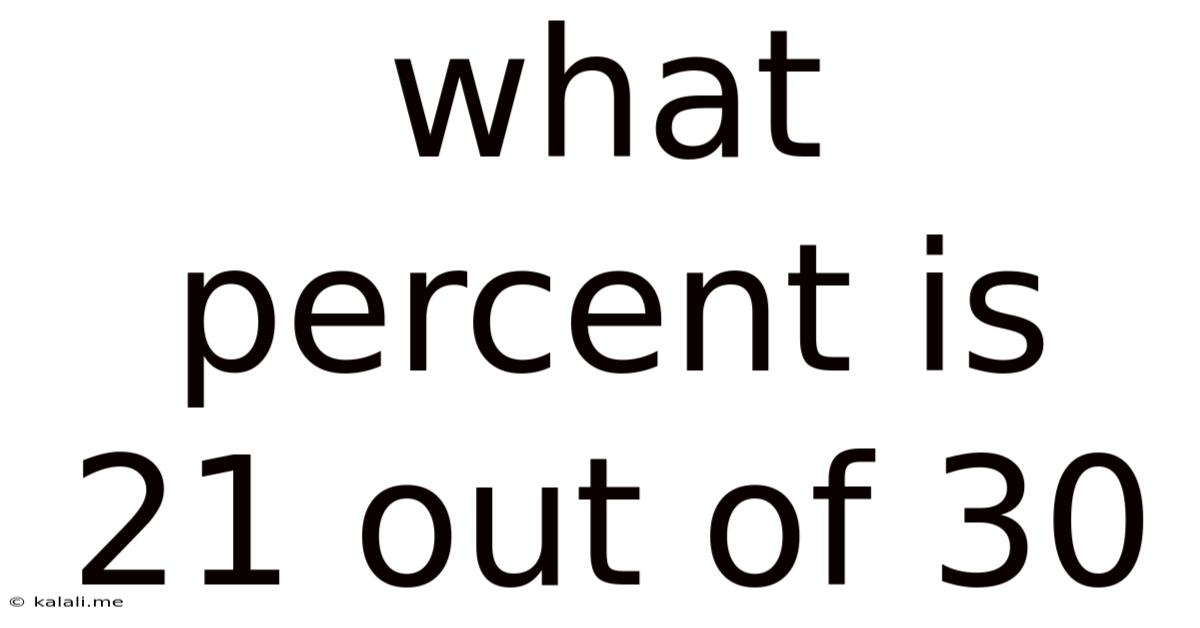
Table of Contents
What Percent is 21 out of 30? A Comprehensive Guide to Percentage Calculations
Finding out what percentage 21 is out of 30 might seem like a simple arithmetic problem, but understanding the underlying principles can unlock a powerful tool for various applications, from everyday budgeting to complex data analysis. This comprehensive guide will not only answer the question directly but also delve into the methodology, provide alternative approaches, and explore real-world applications of percentage calculations. This ensures you not only get the answer but also gain a strong grasp of the concept.
Meta Description: Learn how to calculate percentages with this in-depth guide. We solve the problem "What percent is 21 out of 30?" and explore various methods and real-world applications of percentage calculations.
Calculating the Percentage: The Direct Approach
The most straightforward way to determine what percentage 21 represents out of 30 involves a simple formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 21
- Whole: 30
Therefore, the calculation is:
(21 / 30) * 100% = 70%
Therefore, 21 is 70% of 30.
Understanding the Formula: Deconstructing the Percentage Calculation
The formula above might seem self-evident, but understanding its underlying logic is crucial for applying it correctly in diverse scenarios. The division (Part / Whole) determines the proportion of the part relative to the whole. This proportion is then multiplied by 100% to express it as a percentage – a value out of 100. This conversion to a percentage makes it easy to compare proportions across different datasets.
Alternative Methods for Percentage Calculation
While the direct method is efficient, exploring alternative approaches can enhance your understanding and provide flexibility for different problem types.
Method 2: Using Proportions
We can solve this problem using proportions. We set up a proportion where x represents the unknown percentage:
21/30 = x/100
To solve for x, we cross-multiply:
30x = 2100
x = 2100 / 30
x = 70
Therefore, x = 70%, confirming our earlier result. This method is particularly useful when dealing with more complex proportional relationships.
Method 3: Finding the Percentage Increase or Decrease
While this problem doesn't explicitly ask for a percentage increase or decrease, understanding this concept is crucial. Imagine you started with 30 and ended up with 21. This represents a decrease. The formula for percentage decrease is:
(Original Value – New Value) / Original Value * 100%
In our case:
(30 - 21) / 30 * 100% = 9 / 30 * 100% = 30%
This calculation shows a 30% decrease from 30 to 21. This is different from the 70% we calculated earlier because that represented the proportion of 21 relative to 30, not the change from 30 to 21. It's important to differentiate between these two types of percentage calculations.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of life, from finance and business to science and everyday decision-making. Here are some examples:
- Finance: Calculating interest rates, discounts, tax percentages, profit margins, and investment returns. Understanding percentage changes in your savings or investments is crucial for financial planning.
- Business: Analyzing sales figures, market share, customer satisfaction, and operational efficiency. Tracking percentage changes in these metrics helps businesses make informed decisions.
- Science: Expressing experimental results, analyzing data, and representing proportions in various scientific fields. For instance, calculating the percentage of a certain element in a compound.
- Everyday Life: Calculating tips in restaurants, understanding discounts in shops, comparing prices, and interpreting statistics in news reports.
Advanced Percentage Calculations: Handling More Complex Scenarios
While the example of 21 out of 30 is relatively straightforward, let's examine more complex scenarios where understanding percentage calculations becomes even more critical.
Scenario 1: Percentage Change Over Multiple Periods
Imagine your sales increased by 10% in the first quarter and by 15% in the second quarter. Simply adding the percentages (25%) is incorrect. To calculate the overall percentage increase, you must apply the percentages sequentially.
Let's say your initial sales were 100 units.
- After the first quarter: 100 * 1.10 = 110 units
- After the second quarter: 110 * 1.15 = 126.5 units
The overall percentage increase is (126.5 - 100) / 100 * 100% = 26.5%. This demonstrates the importance of careful calculation when dealing with percentage changes over time. This concept is crucial for understanding compound interest, for example.
Scenario 2: Percentage of a Percentage
Sometimes, you need to find a percentage of a percentage. For example, you might need to calculate 20% of 15% of a total amount. This is done by multiplying the percentages as decimals:
0.20 * 0.15 = 0.03 or 3%
This means 20% of 15% is 3%.
Scenario 3: Calculating Weighted Averages with Percentages
Weighted averages use percentages to account for the relative importance of different data points. For example, imagine your grade in a course is based on 70% from exams and 30% from assignments. If you scored 80% on exams and 90% on assignments, your final grade would be:
(0.70 * 80%) + (0.30 * 90%) = 83%
Avoiding Common Mistakes in Percentage Calculations
Several common mistakes can lead to inaccurate results. Being aware of these pitfalls is essential for ensuring the accuracy of your calculations:
- Confusing Percentage Increase/Decrease with Proportion: Remember the difference between calculating the proportion of one number relative to another and calculating the percentage increase or decrease between two numbers.
- Incorrectly Applying Percentage Changes Over Multiple Periods: Don't simply add percentage changes over time; apply them sequentially.
- Misinterpreting Weighted Averages: Ensure you correctly apply the weights to each data point when calculating weighted averages.
- Rounding Errors: Be mindful of rounding errors, particularly when dealing with several percentage calculations.
Conclusion: Mastering Percentage Calculations
Understanding percentage calculations is a fundamental skill applicable across various fields. By mastering the basic formula and understanding the underlying principles, you can effectively tackle a wide range of problems, from simple percentage calculations to more complex scenarios involving percentage changes, weighted averages, and sequential percentage applications. This guide provides a comprehensive overview of percentage calculations, helping you build confidence and accuracy in applying these essential mathematical skills. Remember to always double-check your work and be aware of potential pitfalls to ensure accurate results. The seemingly simple question, "What percent is 21 out of 30?" opens the door to a world of practical and powerful applications of percentage calculations.
Latest Posts
Latest Posts
-
How Many Hours Is 200 Mins
Apr 18, 2025
-
59 Centimeters Is How Many Inches
Apr 18, 2025
-
How Many Liters Is 64 Oz Of Water
Apr 18, 2025
-
What Is 30 Out Of 40
Apr 18, 2025
-
What Percent Is 3 Of 7
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 21 Out Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.