What Percent Is 3 Of 12
Kalali
Mar 30, 2025 · 4 min read
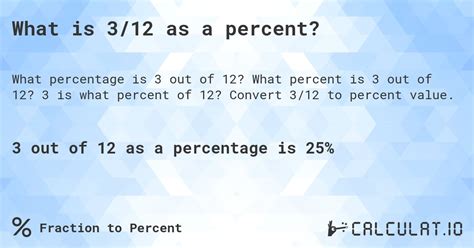
Table of Contents
What Percent is 3 of 12? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous areas of life, from calculating discounts and tips to analyzing data and understanding financial reports. This comprehensive guide will delve into the question, "What percent is 3 of 12?", and explore the broader concepts of percentage calculations, offering various methods and real-world examples to solidify your understanding.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" (from the Latin per centum). Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Calculating "What Percent is 3 of 12?"
Let's tackle the core question: What percentage is 3 out of 12? We can solve this using several methods:
Method 1: Using the Formula
The basic formula for calculating percentages is:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 3
- Whole: 12
Substituting these values into the formula:
(3 / 12) * 100% = 0.25 * 100% = 25%
Therefore, 3 is 25% of 12.
Method 2: Simplifying the Fraction
Before multiplying by 100%, we can simplify the fraction 3/12:
3/12 can be simplified by dividing both the numerator (3) and the denominator (12) by their greatest common divisor, which is 3:
3 ÷ 3 = 1 12 ÷ 3 = 4
This simplifies the fraction to 1/4. Now, we convert this fraction to a percentage:
(1 / 4) * 100% = 0.25 * 100% = 25%
This confirms that 3 is 25% of 12.
Method 3: Using Proportions
We can also solve this using proportions. We set up a proportion where x represents the unknown percentage:
3/12 = x/100
To solve for x, we cross-multiply:
12x = 300
Then, we divide both sides by 12:
x = 300 / 12 = 25
Therefore, x = 25%, confirming our previous results.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various everyday situations:
1. Discounts and Sales
Retail stores frequently advertise discounts as percentages. For instance, a "20% off" sale means you pay 80% of the original price. If an item costs $50 and is 20% off, the discount is (20/100) * $50 = $10, and the final price is $40.
2. Taxes and Tips
Sales taxes and service tips are often expressed as percentages. If the sales tax is 6% and your purchase is $75, the tax amount is (6/100) * $75 = $4.50, bringing the total cost to $79.50. Similarly, a 15% tip on a $100 meal would be (15/100) * $100 = $15.
3. Financial Analysis
Percentages are fundamental in financial statements. Profit margins, return on investment (ROI), and interest rates are all expressed as percentages. Analyzing these percentages helps assess the financial health and performance of businesses and investments.
4. Data Analysis and Statistics
Percentages are widely used in data analysis and statistics to represent proportions and trends. For example, survey results are often presented as percentages to show the distribution of responses. Understanding these percentages allows for better interpretation and insights from the data.
Beyond the Basics: More Complex Percentage Problems
While the "What percent is 3 of 12?" example is straightforward, percentage calculations can become more complex. Let's explore some variations:
Finding the Whole when given the Part and Percentage
Suppose you know that 20% of a number is 10. To find the whole number, we can use the formula:
Whole = (Part / Percentage) * 100
Substituting the values:
Whole = (10 / 20) * 100 = 50
Therefore, the whole number is 50.
Finding the Part when given the Whole and Percentage
If you know that 30% of a number is 15, how do you find 30% of it?
Part = (Percentage / 100) * Whole
Here:
Part = (30/100) * 15 = 4.5
Therefore, 30% of 15 is 4.5
Percentage Increase and Decrease
Percentage increase and decrease are commonly used to show changes over time.
Percentage Increase = [(New Value - Old Value) / Old Value] * 100%
Percentage Decrease = [(Old Value - New Value) / Old Value] * 100%
For example, if a stock price rises from $10 to $12, the percentage increase is [(12 - 10) / 10] * 100% = 20%. If the price falls from $12 to $9, the percentage decrease is [(12 - 9) / 12] * 100% = 25%.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: The more you practice, the more comfortable you'll become with percentage calculations.
-
Use a Calculator: For more complex problems, a calculator can significantly speed up the process.
-
Understand the Fundamentals: A strong grasp of fractions and decimals is essential for mastering percentages.
-
Check Your Work: Always double-check your calculations to ensure accuracy.
-
Visual Aids: Using diagrams or charts can help visualize percentage problems and make them easier to understand.
-
Real-World Application: Apply your knowledge of percentages to real-life scenarios to reinforce your learning.
By understanding the principles discussed above and practicing regularly, you'll build confidence and proficiency in solving various percentage problems, including those beyond the simple "What percent is 3 of 12?" example. Remember that mastering percentages is a valuable skill applicable to numerous aspects of life.
Latest Posts
Latest Posts
-
How Many Feet Is 136 Inches
Apr 01, 2025
-
How Many Kilometers Is 3 Miles
Apr 01, 2025
-
Common Multiples Of 4 And 5
Apr 01, 2025
-
What Is 0 125 As A Fraction
Apr 01, 2025
-
12 Out Of 14 As A Percentage
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 3 Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
