What Percent Is 36 Out Of 50
Kalali
Apr 18, 2025 · 5 min read
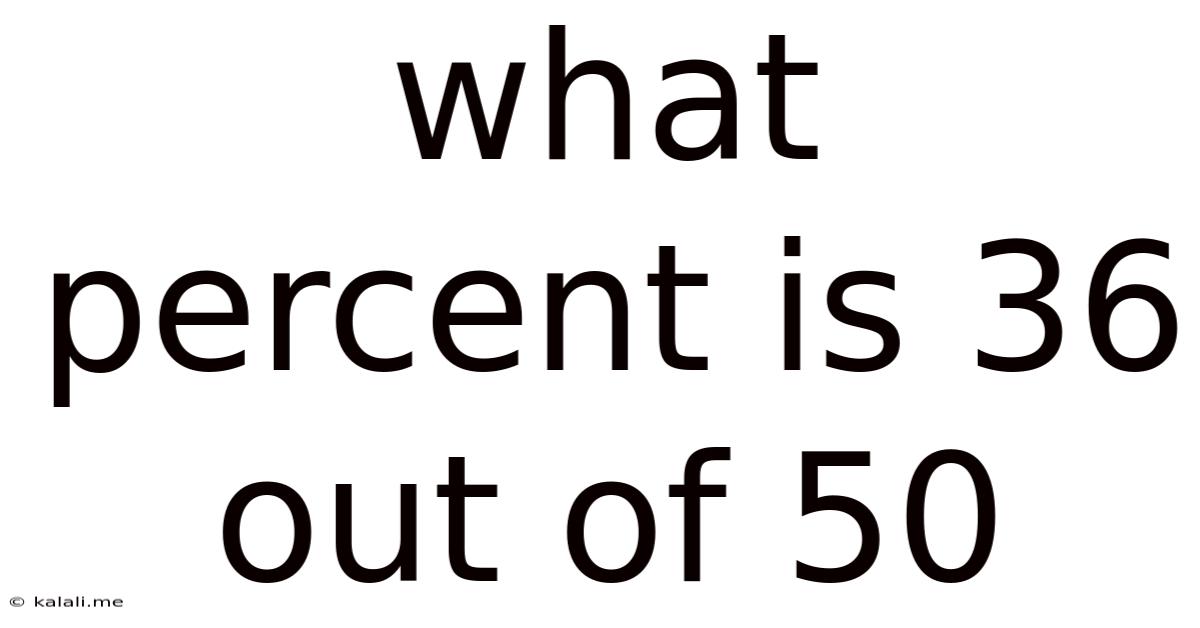
Table of Contents
What Percent is 36 Out of 50? A Deep Dive into Percentage Calculations and Real-World Applications
Knowing how to calculate percentages is a fundamental skill applicable across numerous aspects of life, from academic assessments and financial planning to understanding data analysis and everyday comparisons. This article will thoroughly explore the question "What percent is 36 out of 50?" and, more broadly, provide a comprehensive guide to understanding and calculating percentages effectively. We’ll delve into the mathematical process, discuss various methods of calculation, and explore practical examples demonstrating the relevance of percentage calculations in various contexts. This will include exploring related concepts like ratios, proportions, and fractions, solidifying your understanding of percentage calculations and their importance.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to find what percent 36 is out of 50. This guide covers different methods, real-world examples, and related concepts like ratios and proportions, making percentage calculations easy to understand.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 10% means 10 out of 100, which can be written as the fraction 10/100 or the decimal 0.10. Understanding this fundamental concept is crucial for any percentage calculation.
Method 1: The Direct Calculation Method
The most straightforward approach to determine what percent 36 is out of 50 involves setting up a proportion:
- 36/50 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
- 50x = 3600
Then, we divide both sides by 50:
- x = 3600/50 = 72
Therefore, 36 out of 50 is 72%.
Method 2: Using Decimal Conversion
Another method involves first converting the fraction 36/50 into a decimal. We divide 36 by 50:
- 36 ÷ 50 = 0.72
To express this decimal as a percentage, we multiply by 100:
- 0.72 × 100 = 72%
This again confirms that 36 out of 50 is 72%. This method is particularly useful when using calculators, as it streamlines the calculation process.
Method 3: Simplifying the Fraction
Before performing the division, we can simplify the fraction 36/50 by finding the greatest common divisor (GCD) of 36 and 50, which is 2. Dividing both the numerator and denominator by 2, we get:
- 36/50 = 18/25
Now, we convert the simplified fraction to a decimal by dividing 18 by 25:
- 18 ÷ 25 = 0.72
Finally, multiply the decimal by 100 to obtain the percentage:
- 0.72 × 100 = 72%
This method demonstrates that simplifying fractions can sometimes simplify the subsequent calculations.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is incredibly valuable in numerous real-world scenarios. Here are a few examples:
-
Academic Performance: If a student scores 36 out of 50 on a test, they have achieved 72%, providing a clear understanding of their performance. This allows for easy comparison across different tests and subjects.
-
Financial Calculations: Percentages are fundamental in understanding interest rates, discounts, taxes, and investment returns. For example, calculating the percentage increase or decrease in your savings account balance or determining the final price after a discount involves percentage calculations.
-
Data Analysis: In many fields, data is often presented as percentages to allow for easy comparison and interpretation. For instance, understanding market share, survey results, or the success rate of a particular process requires calculating percentages. This simplifies the interpretation of complex datasets.
-
Sales and Marketing: Businesses use percentages extensively to track sales figures, conversion rates, customer retention, and marketing campaign effectiveness. Calculating percentages helps businesses understand what strategies are working and where improvements are needed.
-
Everyday Comparisons: Comparing prices, quantities, or proportions often involves percentages. For example, comparing the relative sizes of two items, determining the best deal on groceries, or understanding nutrition labels all require percentage understanding.
Understanding Ratios and Proportions
Percentages are closely related to ratios and proportions. A ratio is a comparison of two numbers, often expressed as a fraction. A proportion is a statement that two ratios are equal. The calculation we performed earlier, 36/50 = x/100, is a classic example of a proportion used to solve for a percentage. Understanding ratios and proportions strengthens your ability to solve a wide range of percentage problems.
Advanced Percentage Calculations
While the example of 36 out of 50 is relatively straightforward, many percentage problems involve more complex scenarios. Here are a few examples of more advanced calculations:
-
Calculating Percentage Increase or Decrease: This involves finding the percentage change between two numbers. The formula is: [(New Value - Old Value) / Old Value] × 100%.
-
Calculating Percentage of a Percentage: This involves finding a percentage of a given percentage, which requires performing multiple percentage calculations sequentially.
-
Finding the Original Value: This type of problem requires working backward from a percentage to determine the original value before a percentage increase or decrease was applied. This often involves solving algebraic equations.
Mastering Percentage Calculations: Tips and Tricks
Mastering percentage calculations requires practice and a solid understanding of the underlying concepts. Here are some tips to help you improve:
-
Practice Regularly: The more you practice, the more comfortable you will become with the calculations.
-
Use Different Methods: Experiment with various calculation methods to find the approach that suits you best.
-
Understand the Concepts: Ensure you fully grasp the concepts of ratios, proportions, fractions, and decimals before tackling complex percentage problems.
-
Check Your Work: Always double-check your calculations to avoid errors.
-
Use Online Resources: Numerous online calculators and tutorials can assist you with percentage calculations and provide additional practice.
Conclusion
Understanding how to calculate percentages is a fundamental life skill. The question "What percent is 36 out of 50?" provides a simple yet valuable entry point into a wide world of percentage calculations and their practical applications. By mastering these calculations and understanding related concepts like ratios and proportions, you equip yourself with a powerful tool applicable in various academic, professional, and personal contexts. Remember that consistent practice and a firm grasp of the underlying mathematical principles are key to success in mastering this essential skill. From analyzing data to making financial decisions, the ability to confidently calculate percentages empowers you to navigate the numerical world with increased clarity and understanding.
Latest Posts
Latest Posts
-
How Many Centimeters Are In 10 Meters
Apr 19, 2025
-
What Are The Factors Of 88
Apr 19, 2025
-
Convertir Metros En Pulgadas Y Pies
Apr 19, 2025
-
What Percent Is 3 Out Of 15
Apr 19, 2025
-
Cuantas Pulgadas Hay En 6 Pies
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 36 Out Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.