What Percent Is 5 Of 8
Kalali
Mar 29, 2025 · 5 min read
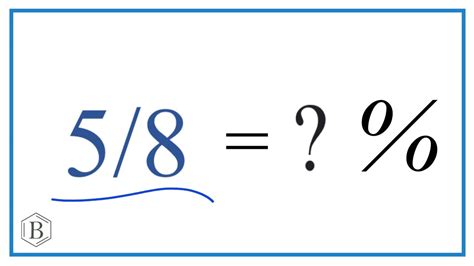
Table of Contents
What Percent is 5 of 8? A Deep Dive into Percentage Calculations
Determining what percentage 5 represents of 8 might seem like a simple arithmetic problem, but understanding the underlying concepts and various methods of calculation is crucial for anyone navigating the world of percentages. This comprehensive guide delves into not only the solution but also the broader implications and applications of percentage calculations in various fields. We will explore multiple approaches, ensuring you master this fundamental concept.
Understanding Percentages: The Foundation
Before we tackle the specific problem of "What percent is 5 of 8?", let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a portion of 100. The term "percent" literally means "per hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Method 1: The Direct Proportion Method
This is arguably the most straightforward method for solving "What percent is 5 of 8?". We can set up a proportion:
- 5/8 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
- 8x = 500
Then, divide both sides by 8:
- x = 500/8 = 62.5
Therefore, 5 is 62.5% of 8.
Method 2: Using Decimal Conversion
This method involves converting the fraction 5/8 into a decimal and then multiplying by 100 to express it as a percentage.
- Divide 5 by 8: 5 ÷ 8 = 0.625
- Multiply the decimal by 100: 0.625 × 100 = 62.5%
This method provides the same result: 5 is 62.5% of 8.
Method 3: Understanding the Concept of "Part," "Whole," and "Percentage"
This approach focuses on understanding the relationship between the three key components of a percentage problem:
- Part: The portion we're interested in (in this case, 5).
- Whole: The total amount (in this case, 8).
- Percentage: The fraction of the whole represented by the part (what we need to find).
The formula to find the percentage is:
(Part / Whole) x 100 = Percentage
Substituting our values:
(5 / 8) x 100 = 62.5%
This method reinforces the fundamental concept and makes the calculation transparent.
Real-World Applications of Percentage Calculations
Understanding percentage calculations isn't just about solving mathematical problems; it's a crucial skill applicable to numerous real-world scenarios:
- Finance: Calculating interest rates, discounts, profits, and losses. For instance, a 10% discount on an $80 item is calculated as (10/100) * $80 = $8.
- Retail: Determining profit margins, sales tax, and markups. A retailer might mark up an item by 50% to achieve a desired profit margin.
- Science: Expressing experimental results, representing statistical data, and calculating concentrations of solutions. For example, a solution might contain 25% of a specific compound.
- Everyday Life: Calculating tips, determining the percentage of completion of a task, understanding nutritional information on food labels (e.g., percentage of daily recommended value).
Beyond the Basics: Advanced Percentage Calculations
While finding what percent 5 is of 8 is relatively straightforward, let's explore some more complex scenarios involving percentages:
- Finding the Whole: If 20% of a number is 10, what is the number? This requires rearranging the percentage formula: Whole = (Part / Percentage) x 100. So, Whole = (10 / 20) x 100 = 50.
- Finding the Part: If 30% of a number is 15, what is 60% of that number? First, find the whole number (as shown above), and then calculate 60% of that number.
- Percentage Increase/Decrease: Calculating percentage change involves finding the difference between two values and then expressing this difference as a percentage of the original value. For example, if a price increases from $50 to $60, the percentage increase is [(60-50)/50] x 100 = 20%.
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest over a period. Understanding compound interest is critical for planning long-term investments.
Troubleshooting Common Percentage Mistakes
Many errors in percentage calculations stem from misunderstandings of the fundamental concepts or simple arithmetic errors. Here are some common mistakes to avoid:
- Incorrectly identifying the part and the whole: Always carefully define which number represents the part and which represents the whole.
- Forgetting to multiply by 100: Remember that the final step in calculating a percentage is multiplying the decimal result by 100.
- Misinterpreting percentage increase/decrease: Make sure you're calculating the change relative to the original value, not the new value.
- Using incorrect formulas: Double-check that you're using the appropriate formula for the type of percentage problem you're solving.
Improving Your Percentage Calculation Skills
Practice is key to mastering percentage calculations. Work through various problems, starting with simple examples like "What percent is 5 of 8?" and gradually progressing to more complex scenarios. Use different methods to solve the same problem to reinforce your understanding and identify the most efficient approach for you. Online resources, textbooks, and practice exercises can provide ample opportunities for honing your skills.
Conclusion: Mastering Percentages for Success
Understanding percentages is a fundamental skill applicable across diverse fields. By grasping the core concepts, mastering various calculation methods, and avoiding common mistakes, you can confidently tackle percentage problems in your academic pursuits, professional life, and everyday decisions. Remember that practice and a solid understanding of the underlying principles are the keys to success in this critical area of mathematics. The seemingly simple question, "What percent is 5 of 8?", serves as a gateway to a world of practical applications and problem-solving capabilities. Continue to explore and expand your knowledge, and you'll find percentages becoming increasingly intuitive and manageable.
Latest Posts
Latest Posts
-
How Many Feet Is 130 Cm
Mar 31, 2025
-
How Many Inches Is 25 Centimeters
Mar 31, 2025
-
How Long Is 2 Hours In Minutes
Mar 31, 2025
-
What Is 20 Of 70 Dollars
Mar 31, 2025
-
What Is 3 20 As A Percentage
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 5 Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
