What Percent Is 6 Out Of 10
Kalali
Apr 27, 2025 · 5 min read
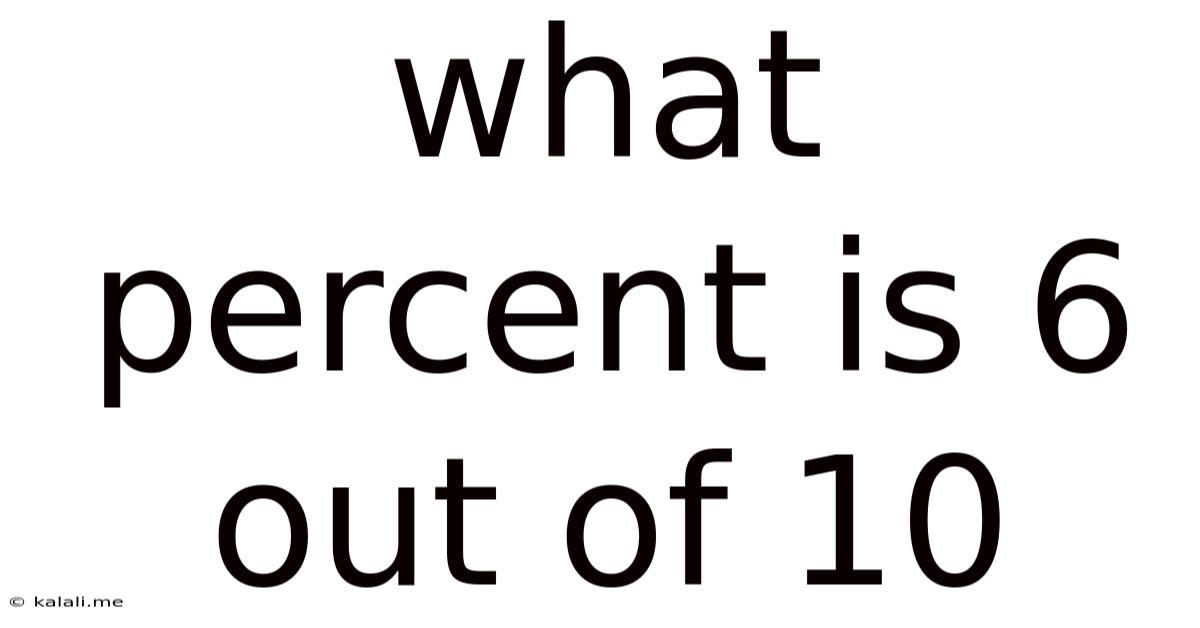
Table of Contents
What Percent is 6 out of 10? A Deep Dive into Percentages and Their Applications
Meta Description: Learn how to calculate percentages, understand what 6 out of 10 represents as a percentage, and explore real-world applications of percentage calculations. This comprehensive guide covers basic percentage concepts and advanced applications.
Understanding percentages is a fundamental skill applicable across numerous fields, from everyday finances to complex scientific analyses. This article will thoroughly explore the question "What percent is 6 out of 10?" and then delve into the broader topic of percentage calculations, providing practical examples and applications.
Calculating the Percentage: 6 out of 10
The simplest way to calculate what percentage 6 out of 10 represents is to use the following formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 6 (the number we're interested in)
- Whole: 10 (the total number)
Substituting these values into the formula, we get:
(6 / 10) x 100% = 60%
Therefore, 6 out of 10 is 60%.
This calculation is straightforward, but understanding the underlying concepts is crucial for applying percentage calculations in more complex scenarios.
Understanding Percentages: A Fundamental Concept
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Percentages provide a standardized way to compare proportions and make numerical data easier to understand and interpret. They are used extensively in various fields, including:
- Finance: Interest rates, discounts, taxes, investment returns, and profit margins are all expressed as percentages.
- Science: Scientific data analysis often involves representing results as percentages, allowing for easy comparison and interpretation of experimental outcomes. For example, the success rate of a treatment or the percentage of a certain element in a compound.
- Statistics: Percentages are critical for summarizing and presenting data, particularly when dealing with large datasets. Think of polls, surveys and demographic analysis.
- Education: Grades, test scores, and class attendance are often reported as percentages.
- Everyday Life: Sales discounts, tip calculations, and understanding nutritional information on food labels all involve percentage calculations.
Beyond the Basics: More Complex Percentage Problems
While calculating 6 out of 10 is relatively simple, more complex problems require a deeper understanding of percentage calculations. Let's explore some common scenarios:
1. Finding the Percentage Increase or Decrease:
This involves determining the percentage change between two values. The formula is:
[(New Value - Original Value) / Original Value] x 100% = Percentage Change
For example, if the price of a product increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] x 100% = 20%
2. Finding a Percentage of a Number:
This involves calculating a specific percentage of a given number. The formula is:
(Percentage / 100) x Number = Result
For example, to find 25% of 80, the calculation is:
(25 / 100) x 80 = 20
3. Finding the Original Number Given a Percentage:
This involves working backward from a percentage to find the original number. For instance, if 20% of a number is 10, what is the original number? We can set up the equation:
(20/100) * x = 10
Solving for x (the original number), we get:
x = 10 / (20/100) = 50
4. Calculating Percentage Points:
Percentage points represent the arithmetic difference between two percentages, not the percentage difference. For example, an increase from 10% to 15% is a 5-percentage-point increase, but a 50% increase (5/10 * 100%). This distinction is crucial when interpreting data, especially in financial reports or economic statistics.
Practical Applications of Percentage Calculations
The applications of percentage calculations are vast and varied. Let's consider some real-world examples:
- Financial Planning: Calculating interest earned on savings accounts, determining the cost of a loan, budgeting expenses, and tracking investment returns all rely heavily on percentage calculations. For example, understanding compound interest and how it affects long-term savings requires a solid grasp of percentages.
- Sales and Marketing: Analyzing sales figures, calculating discounts and markups, measuring the effectiveness of advertising campaigns, and setting profit margins all necessitate the use of percentages. For instance, understanding conversion rates (the percentage of visitors to a website who make a purchase) is critical for online businesses.
- Data Analysis and Interpretation: Percentages are indispensable for summarizing and interpreting data in various fields. In surveys, for instance, reporting results as percentages facilitates clear communication of findings. Analyzing statistical data and drawing meaningful conclusions frequently involve percentage calculations.
- Healthcare: Calculating the success rate of treatments, measuring the prevalence of diseases, and monitoring patient progress often involve percentages. For example, understanding mortality rates or the effectiveness of a new drug requires percentage calculations.
- Education: Assessing student performance using grades (which are often expressed as percentages), analyzing test scores, and tracking student attendance all rely on percentage calculations.
Advanced Percentage Concepts
While the basic percentage formula provides a strong foundation, more advanced concepts include:
- Compound Interest: Interest earned not only on the principal amount but also on the accumulated interest from previous periods. This leads to exponential growth over time, a significant concept in finance and investment.
- Weighted Averages: Used when different values contribute to the overall average in varying proportions. For instance, calculating a final grade based on different assignment weights.
- Percentage Points vs. Percentage Change: Understanding the difference between these two concepts is crucial for accurate interpretation of data, especially when comparing changes in percentages over time.
- Statistical Significance: In statistical analysis, percentages are used to determine the statistical significance of results, indicating the likelihood that observed differences are not due to random chance.
Conclusion: Mastering Percentages for Success
Understanding percentages is a vital skill in many aspects of life, from managing personal finances to interpreting complex data sets. While calculating something like "what percent is 6 out of 10?" is relatively simple, mastering percentage calculations allows you to tackle more complex problems and confidently analyze data in various contexts. The ability to work with percentages effectively empowers you to make informed decisions and enhances your understanding of the numerical world around you. This comprehensive understanding of percentages extends far beyond simple arithmetic; it’s a tool that unlocks deeper insights and more effective decision-making across a wide range of fields.
Latest Posts
Latest Posts
-
What Is The Percentage Of 0 1
Apr 28, 2025
-
What Is 0 02 As A Percent
Apr 28, 2025
-
How Many Feet Is 178 Inches
Apr 28, 2025
-
What Is 0 03 As A Fraction
Apr 28, 2025
-
What Percent Is 4 Out Of 6
Apr 28, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 6 Out Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.