What Percent Is 80 Of 200
Kalali
Apr 01, 2025 · 4 min read
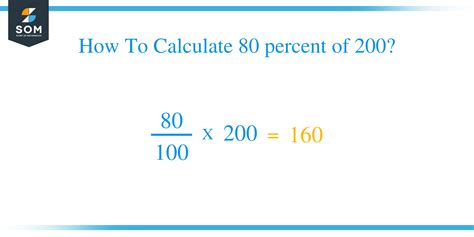
Table of Contents
What Percent is 80 of 200? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous areas of life, from calculating discounts in a store to analyzing financial reports. This comprehensive guide will not only answer the question, "What percent is 80 of 200?" but will also equip you with the knowledge and techniques to confidently tackle any percentage problem.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Understanding this fundamental concept is crucial for mastering percentage calculations.
Calculating Percentages: The Formula
The basic formula for calculating percentages is:
(Part / Whole) x 100% = Percentage
Where:
- Part: Represents the number you want to express as a percentage of the whole.
- Whole: Represents the total amount or the base value.
- Percentage: The result, expressed as a percentage.
Solving "What percent is 80 of 200?"
Now, let's apply this formula to answer our core question: "What percent is 80 of 200?"
In this case:
- Part = 80
- Whole = 200
Substituting these values into the formula:
(80 / 200) x 100% = Percentage
This simplifies to:
(0.4) x 100% = 40%
Therefore, 80 is 40% of 200.
Beyond the Basics: Different Approaches and Scenarios
While the above method is straightforward, let's explore alternative approaches and scenarios to solidify your understanding of percentage calculations.
Method 2: Using Proportions
Percentage problems can also be solved using proportions. A proportion is an equation stating that two ratios are equal. We can set up a proportion as follows:
x / 100 = 80 / 200
Where 'x' represents the percentage we're trying to find. To solve for 'x', we can cross-multiply:
200x = 8000
x = 8000 / 200
x = 40
Therefore, x = 40%. This method confirms our previous result.
Scenario 1: Finding the Part
Let's reverse the problem. Suppose we know that 25% of a number is 50. How do we find the whole number? We can modify the percentage formula:
(Part / Whole) x 100% = Percentage
Rearranging the formula to solve for the whole:
Whole = (Part / Percentage) x 100%
Substituting the values:
Whole = (50 / 25) x 100
Whole = 2 x 100
Whole = 200
Therefore, the whole number is 200.
Scenario 2: Finding the Percentage Increase or Decrease
Percentage increase and decrease calculations are common in various fields, such as finance and statistics. Let's say a product's price increased from $100 to $120. What is the percentage increase?
- Find the difference: $120 - $100 = $20
- Divide the difference by the original value: $20 / $100 = 0.2
- Multiply by 100%: 0.2 x 100% = 20%
Therefore, the price increased by 20%. Similar calculations apply to percentage decrease.
Scenario 3: Applying Percentages to Real-World Problems
Percentage calculations are ubiquitous in real life. Consider these examples:
- Sales Tax: If the sales tax is 6% and you buy an item for $50, the tax amount is (6/100) * $50 = $3. The total cost is $50 + $3 = $53.
- Discounts: A 20% discount on a $150 item means the discount is (20/100) * $150 = $30. The final price is $150 - $30 = $120.
- Interest Rates: Understanding interest rates involves percentage calculations. If you deposit $1000 in a savings account with a 5% annual interest rate, you'll earn (5/100) * $1000 = $50 in interest after one year (assuming simple interest).
- Tips and Gratuities: Calculating tips at restaurants often involves estimating percentages. A 15% tip on a $75 bill would be approximately (15/100) * $75 = $11.25.
- Grade Calculations: Many grading systems use percentages to represent a student's performance. A score of 85 out of 100 translates to an 85% grade.
Advanced Percentage Calculations and Tips
While the basic formula covers many scenarios, some problems require more advanced techniques:
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest from previous periods.
- Percentage Change over Multiple Periods: Calculating the overall percentage change over multiple increases or decreases requires careful consideration of the base value for each period.
- Using Spreadsheets and Software: Spreadsheets like Microsoft Excel and Google Sheets provide built-in functions for percentage calculations, simplifying complex problems.
Practicing Your Percentage Skills
The key to mastering percentage calculations is consistent practice. Start with simple problems and gradually work towards more complex ones. You can find numerous online resources, workbooks, and practice problems to enhance your skills. Try creating your own word problems using real-life scenarios to make the learning more engaging and relevant.
Conclusion: Mastering the World of Percentages
Understanding percentages is a crucial life skill with far-reaching applications. By grasping the fundamental formula, exploring different approaches, and practicing regularly, you can confidently tackle any percentage problem, from the simple "What percent is 80 of 200?" to more complex scenarios. This enhanced understanding will undoubtedly prove valuable in various aspects of your personal and professional life. Remember to utilize the different methods described here to improve your problem-solving abilities and approach percentage calculations with greater confidence. The more you practice, the easier it will become!
Latest Posts
Latest Posts
-
How Many Inches Is 178 Mm
Apr 02, 2025
-
What Is The Number Under The Element
Apr 02, 2025
-
Cuantas Tazas Es Un Litro De Agua
Apr 02, 2025
-
How Many Feet Are In 1 7 Meters
Apr 02, 2025
-
How Many Cups In 5 Quarts Of Water
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 80 Of 200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
