What Percent Of 12 Is 5
Kalali
Apr 27, 2025 · 5 min read
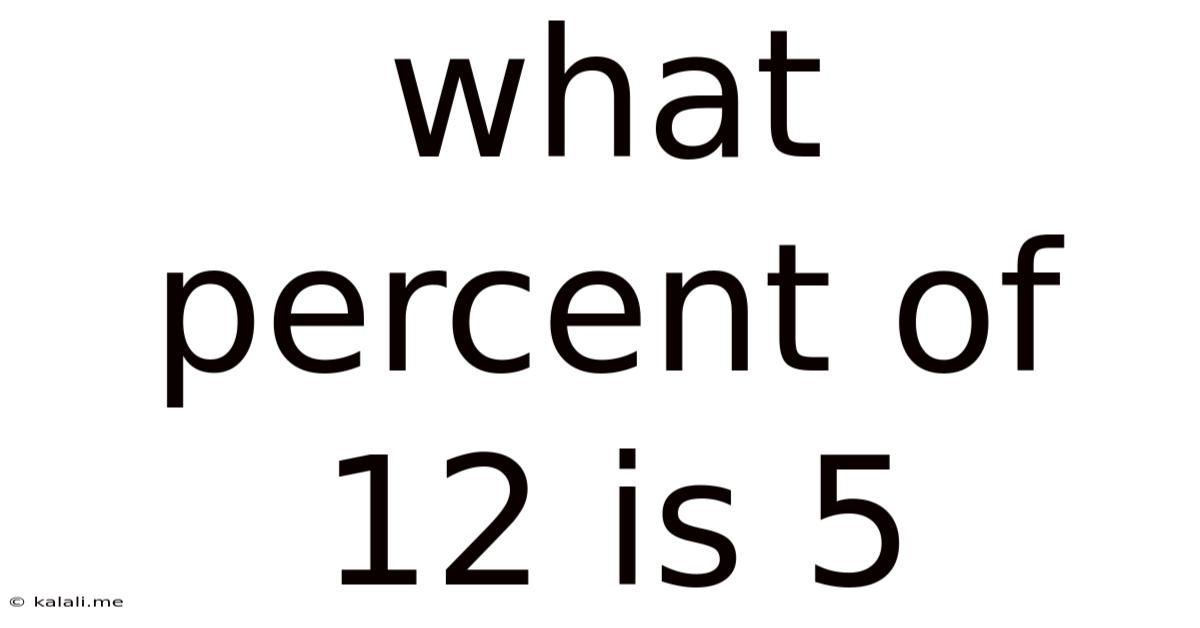
Table of Contents
What Percent of 12 is 5? A Deep Dive into Percentage Calculations
This seemingly simple question – "What percent of 12 is 5?" – opens the door to a broader understanding of percentages, their applications, and the various methods used to solve percentage problems. This article will not only answer the question directly but will also explore the underlying mathematical concepts, different calculation approaches, and practical real-world examples. Understanding percentages is crucial in various fields, from finance and budgeting to statistics and data analysis. By the end of this article, you'll be able to confidently tackle any percentage problem.
Meta Description: Learn how to calculate what percent of 12 is 5. This comprehensive guide explores various methods, real-world applications, and the underlying mathematical principles of percentage calculations. Master percentage problems with ease!
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" is used to denote percentage. Essentially, it represents a portion of a whole. For example, 50% means 50 out of 100, which simplifies to 1/2 or 0.5. Understanding this fundamental concept is key to solving percentage problems.
Method 1: Using the Formula
The most straightforward method to determine what percent of 12 is 5 involves a simple formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 5 (the number we're interested in finding the percentage of)
- Whole: 12 (the total number)
Plugging the values into the formula:
(5 / 12) * 100% ≈ 41.67%
Therefore, 5 is approximately 41.67% of 12.
Method 2: Setting up a Proportion
Another effective method is to set up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as:
5/12 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
12x = 500
x = 500 / 12
x ≈ 41.67
Again, this confirms that 5 is approximately 41.67% of 12.
Method 3: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100%.
First, express the ratio as a decimal:
5 / 12 ≈ 0.4167
Then, multiply by 100% to get the percentage:
0.4167 * 100% ≈ 41.67%
This reinforces the result obtained using the previous methods.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in many real-life situations. Here are a few examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For instance, understanding the interest rate on a loan or the discount percentage on a sale is crucial for making informed financial decisions. Calculating your savings rate or your investment growth in percentage terms helps you track your financial progress.
-
Sales and Marketing: Analyzing sales figures, conversion rates, customer retention, and market share often involves calculating percentages. Marketing campaigns rely on metrics that are expressed as percentages, like click-through rates (CTR) and conversion rates. This data helps businesses understand their campaign effectiveness and make data-driven decisions.
-
Statistics and Data Analysis: Percentages are used extensively in statistics to represent proportions within datasets, making it easier to interpret and compare data. For example, analyzing survey results, calculating the percentage of respondents who favor a particular option provides valuable insights.
-
Education: Grading systems frequently use percentages to represent a student's performance. Calculating the percentage of correct answers on a test helps to assess understanding of the material. Moreover, calculating GPA (Grade Point Average) involves a weighted percentage calculation.
-
Everyday Life: Calculating tips in restaurants, determining sale prices, understanding nutritional information on food labels, and even figuring out the percentage of tasks completed in a project all involve using percentages.
Advanced Percentage Problems and Solutions
While the initial problem was relatively simple, percentage calculations can become more complex. Let's explore some more challenging scenarios and how to approach them:
Scenario 1: Finding the Whole when given the Part and Percentage
Problem: 25% of what number is 10?
Solution: We can use the formula:
(Part / Percentage) * 100 = Whole
(10 / 25) * 100 = 40
Therefore, 25% of 40 is 10.
Scenario 2: Finding the Part when given the Whole and Percentage
Problem: What is 60% of 80?
Solution: We can use the formula:
(Percentage / 100) * Whole = Part
(60 / 100) * 80 = 48
Therefore, 60% of 80 is 48.
Scenario 3: Percentage Increase or Decrease
Problem: A product's price increased from $50 to $60. What is the percentage increase?
Solution: First, calculate the difference: $60 - $50 = $10.
Then, divide the difference by the original price and multiply by 100%:
($10 / $50) * 100% = 20%
The price increased by 20%.
Scenario 4: Successive Percentage Changes
Problem: A price is increased by 10% and then decreased by 10%. Is the final price the same as the original price?
Solution: No. Let's say the original price is $100.
10% increase: $100 + ($100 * 0.10) = $110
10% decrease: $110 - ($110 * 0.10) = $99
The final price is $99, which is less than the original price. This demonstrates that successive percentage changes are not always additive.
Tips and Tricks for Mastering Percentage Calculations
-
Practice Regularly: The more you practice, the more comfortable you'll become with percentage calculations. Start with simple problems and gradually work your way up to more complex ones.
-
Use a Calculator: For more complex calculations, using a calculator can save time and increase accuracy. Many calculators have a percentage function that simplifies the process.
-
Understand the Context: Always carefully read the problem statement and understand the context. This will help you identify the part, the whole, and the percentage accurately.
-
Check Your Work: Always double-check your answers to ensure accuracy. You can do this by using a different method or by working backward from your answer.
-
Break Down Complex Problems: If you're faced with a complex percentage problem, try to break it down into smaller, more manageable steps. This will make the problem easier to solve.
Conclusion
Calculating what percent of 12 is 5, while seemingly straightforward, provides a springboard to understanding the broader world of percentage calculations. Mastering percentages is a valuable skill applicable across numerous fields, from personal finance to advanced statistical analysis. By understanding the various methods, practicing regularly, and applying these principles to real-world scenarios, you can confidently tackle any percentage problem and make informed decisions in various aspects of your life. Remember to always check your work and utilize resources like calculators when dealing with complex calculations. The ability to interpret and manipulate percentages is a fundamental skill that will serve you well in countless situations.
Latest Posts
Latest Posts
-
What Percent Of 10 Is 9
Apr 27, 2025
-
How Do Limiting Factors Affect Organisms In A Community
Apr 27, 2025
-
What Is 54 Inches In Centimeters
Apr 27, 2025
-
How Many Ounces Is 1 4 Pound
Apr 27, 2025
-
How Many Inches In 81 Cm
Apr 27, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 12 Is 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.