What Percent Of 12 Is 9
Kalali
Apr 12, 2025 · 5 min read
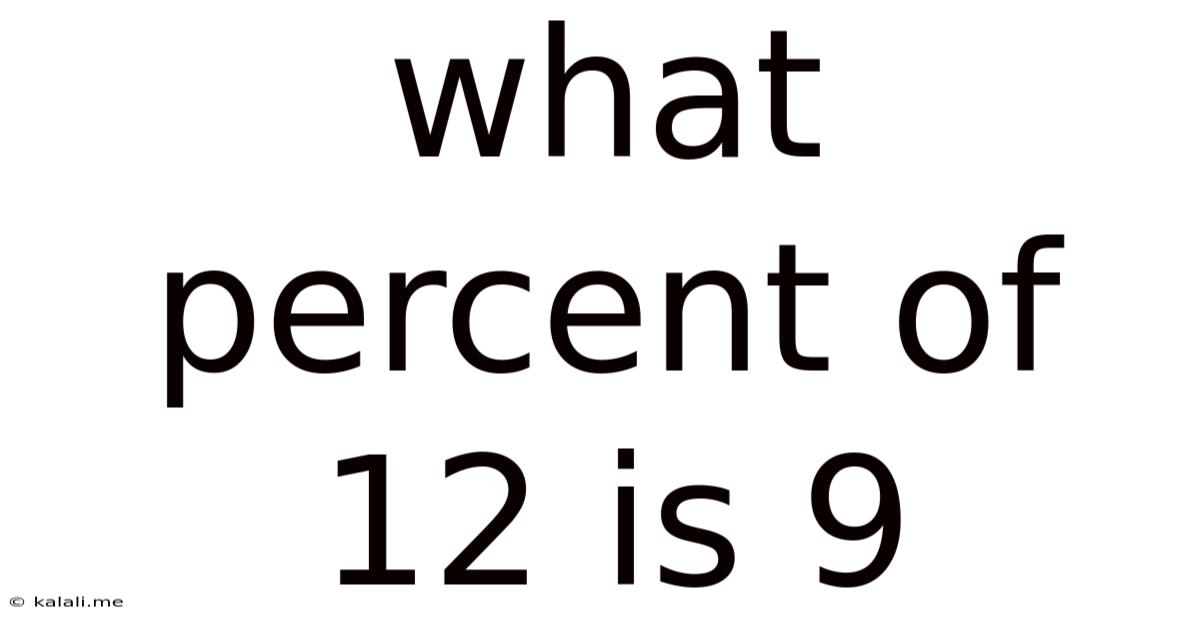
Table of Contents
What Percent of 12 is 9? A Comprehensive Guide to Percentage Calculations
This seemingly simple question – "What percent of 12 is 9?" – opens the door to a deeper understanding of percentages, a fundamental concept in mathematics with wide-ranging applications in everyday life, from calculating discounts and tax to understanding statistics and financial data. This article will not only answer the question but also explore the underlying principles, provide multiple solution methods, and delve into practical applications to solidify your understanding.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to find what percent of 12 is 9. We'll cover multiple methods, practical examples, and real-world applications of percentage calculations.
Understanding Percentages: The Foundation
A percentage is a fraction expressed as a number out of 100. The term "percent" literally means "out of one hundred" (from the Latin "per centum"). When we say "x percent," we're essentially saying "x out of 100," or x/100. This fundamental understanding is crucial for solving percentage problems.
Method 1: Using the Formula
The most straightforward approach to solving "What percent of 12 is 9?" involves using the basic percentage formula:
(Part / Whole) x 100% = Percentage
In our problem:
- Part: 9 (the value we're interested in)
- Whole: 12 (the total value)
Substituting these values into the formula:
(9 / 12) x 100% = 0.75 x 100% = 75%
Therefore, 9 is 75% of 12.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. A proportion is a statement that two ratios are equal. We can express the problem as a proportion:
9/12 = x/100
Where 'x' represents the percentage we're trying to find. To solve for x, we cross-multiply:
9 * 100 = 12 * x
900 = 12x
x = 900 / 12
x = 75
Therefore, x = 75%, confirming our previous result. This method is particularly useful for visualizing the relationship between the parts and the whole.
Method 3: Using Decimal Conversion
This method involves converting the fraction into a decimal and then multiplying by 100%.
First, express the problem as a fraction: 9/12
Then, simplify the fraction: 9/12 simplifies to 3/4
Next, convert the fraction to a decimal by dividing the numerator by the denominator: 3 ÷ 4 = 0.75
Finally, multiply the decimal by 100% to express it as a percentage: 0.75 x 100% = 75%
Practical Applications of Percentage Calculations
The ability to calculate percentages is incredibly useful in numerous real-world scenarios:
-
Retail Discounts: Calculating the final price after a percentage discount. For example, a 20% discount on a $50 item means a reduction of $10 (20% of $50), leaving a final price of $40.
-
Sales Tax: Determining the total cost of an item including sales tax. A 6% sales tax on a $100 purchase adds $6 (6% of $100), resulting in a total cost of $106.
-
Interest Calculations: Calculating simple interest earned on savings accounts or interest paid on loans. For example, 5% interest on a $1000 savings account earns $50 in interest ($1000 x 0.05).
-
Tip Calculation: Determining the appropriate tip amount in restaurants or for service providers. A 15% tip on a $75 bill equals $11.25 (15% of $75).
-
Grade Calculation: Determining the percentage grade achieved on an exam or assignment. Scoring 27 out of 30 on a test results in a 90% grade (27/30 x 100%).
-
Financial Analysis: Analyzing financial statements, such as profit margins, return on investment (ROI), and growth rates, all expressed as percentages.
-
Data Analysis and Statistics: Representing data proportions and trends using percentages in charts, graphs, and reports.
Beyond the Basics: More Complex Percentage Problems
While the question "What percent of 12 is 9?" provides a foundation, percentage calculations can become more complex. Here are a few examples:
-
Finding the Whole: If 25% of a number is 15, what is the number? This requires working backward from the percentage and the part to find the whole.
-
Finding the Part: What is 30% of 80? This involves multiplying the percentage (converted to a decimal) by the whole.
-
Percentage Increase/Decrease: Calculating the percentage change between two values. For example, if a price increases from $50 to $60, the percentage increase is 20%.
Solving More Complex Percentage Problems
Let's illustrate with a more intricate example:
Problem: A store offers a 15% discount on an item originally priced at $80. A 6% sales tax is then added to the discounted price. What is the final price the customer pays?
Solution:
-
Calculate the discount: 15% of $80 = 0.15 * $80 = $12
-
Calculate the discounted price: $80 - $12 = $68
-
Calculate the sales tax: 6% of $68 = 0.06 * $68 = $4.08
-
Calculate the final price: $68 + $4.08 = $72.08
The final price the customer pays is $72.08. This example demonstrates the sequential application of percentage calculations in a real-world scenario.
Mastering Percentages: Tips and Practice
Mastering percentage calculations requires consistent practice and a strong understanding of the underlying principles. Here are some tips to help you:
-
Practice regularly: Solve a variety of percentage problems to build your skills and confidence.
-
Use different methods: Experiment with various solution approaches (formula, proportion, decimal conversion) to find the method that best suits your understanding.
-
Visualize the problem: Draw diagrams or use real-world examples to visualize the relationship between the parts and the whole.
-
Check your work: Always double-check your calculations to ensure accuracy.
-
Utilize online resources: Many online calculators and educational websites provide practice problems and tutorials.
By understanding the basic principles and applying different solution methods, you can confidently tackle any percentage problem, from the simple "What percent of 12 is 9?" to more complex real-world applications. The ability to perform percentage calculations is a valuable skill that will serve you well in various aspects of your life.
Latest Posts
Latest Posts
-
How Many Cm In 2 5 Meters
Apr 18, 2025
-
What Percent Of 60 Is 39
Apr 18, 2025
-
Cuantos Kilometros Hay En Una Milla
Apr 18, 2025
-
18 Ounces Is How Many Grams
Apr 18, 2025
-
What Is 6 Out Of 10 As A Grade
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 12 Is 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.