What Percent Of 120 Is 15
Kalali
Apr 19, 2025 · 5 min read
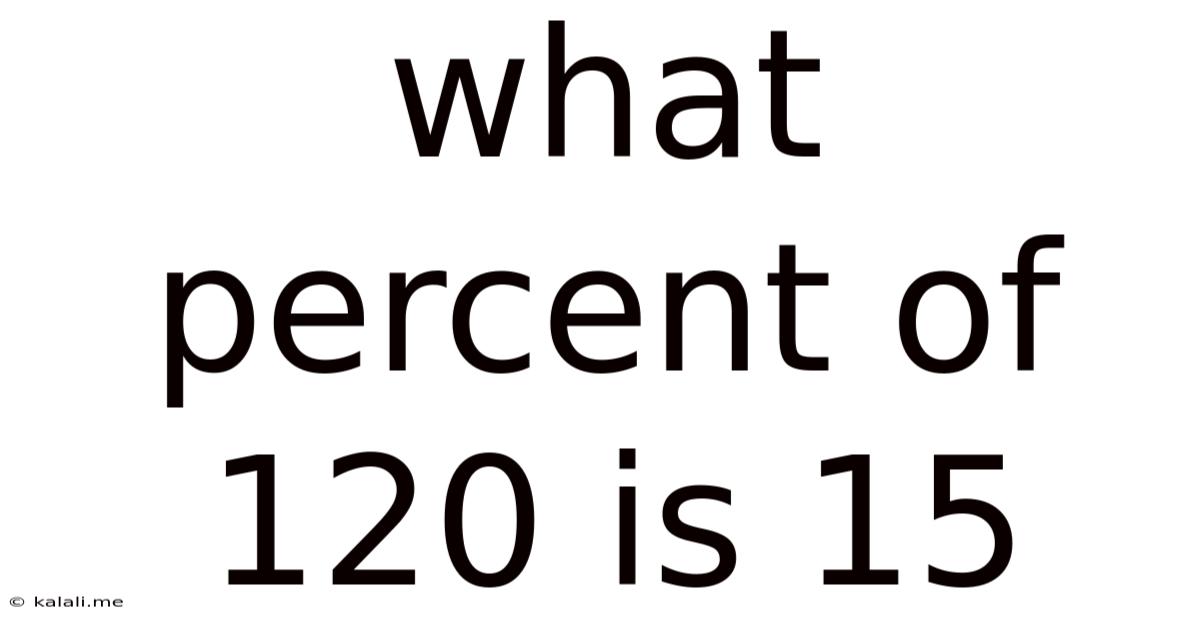
Table of Contents
What Percent of 120 is 15? A Comprehensive Guide to Percentage Calculations
This article delves into the seemingly simple question: "What percent of 120 is 15?" While the answer might seem immediately obvious to some, understanding the underlying principles of percentage calculations is crucial for various applications, from everyday budgeting to complex statistical analysis. We'll explore different methods to solve this problem, discuss the importance of understanding percentages, and provide practical examples to solidify your understanding. This comprehensive guide will empower you to tackle similar percentage problems with confidence.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to find what percent of 120 is 15. We cover multiple methods, practical applications, and real-world examples to master percentage calculations.
Understanding Percentages: A Foundation for Calculation
Before diving into the specific problem, let's establish a firm understanding of what percentages represent. A percentage is simply a fraction expressed as a part of 100. The symbol "%" signifies "per hundred" or "out of 100." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Understanding this fundamental concept is key to solving percentage problems. It allows us to translate word problems into mathematical equations that we can easily solve. The core relationship in percentage problems is always:
(Part / Whole) * 100 = Percentage
In our problem, "What percent of 120 is 15?", we can identify:
- Part: 15 (the smaller quantity)
- Whole: 120 (the larger quantity)
- Percentage: This is what we need to find.
Method 1: Using the Formula Directly
We can directly apply the percentage formula to solve our problem:
(Part / Whole) * 100 = Percentage
(15 / 120) * 100 = Percentage
0.125 * 100 = 12.5%
Therefore, 15 is 12.5% of 120.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. A proportion is a statement that two ratios are equal. We can set up a proportion using the following structure:
Part / Whole = Percentage / 100
Substituting our values:
15 / 120 = x / 100
To solve for 'x' (the percentage), we can cross-multiply:
15 * 100 = 120 * x
1500 = 120x
x = 1500 / 120
x = 12.5
Therefore, 15 is 12.5% of 120.
Method 3: Using Decimal Equivalents
Percentages can easily be converted to decimals by dividing by 100. Conversely, decimals can be converted to percentages by multiplying by 100. We can use this knowledge to solve our problem.
First, let's find what fraction of 120 is 15:
15 / 120 = 0.125
Now, we convert this decimal to a percentage by multiplying by 100:
0.125 * 100 = 12.5%
Again, we find that 15 is 12.5% of 120.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world scenarios. Here are a few examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all involve percentage calculations. For example, calculating the discount on a sale item or determining the amount of interest earned on a savings account.
-
Statistics: Percentages are fundamental in representing and analyzing data. Understanding percentages is crucial for interpreting polls, surveys, and statistical reports. For instance, understanding the percentage of respondents who favor a particular candidate in an election.
-
Science: Percentage calculations are used extensively in scientific experiments and data analysis to express concentrations, error margins, and changes in quantities. Examples include calculating the percentage composition of a chemical compound or the percentage change in population size.
-
Everyday Life: Calculating tips in restaurants, determining sale prices, or understanding nutritional information on food labels involves percentages. For example, determining the amount to tip a waiter based on the bill total or calculating the percentage of daily recommended intake of certain nutrients.
-
Business: In business, percentages are crucial for various aspects, including calculating profit margins, sales growth, market share, and return on investment (ROI). For example, tracking sales growth percentage over different periods.
Advanced Percentage Problems: Building on the Fundamentals
The principles we've covered can be applied to more complex percentage problems. Let's consider some variations:
-
Finding the Whole: If we know the percentage and the part, we can calculate the whole. For instance, if 20% of a number is 30, what is the number? This can be solved by setting up a proportion or using algebraic equations.
-
Finding the Part: If we know the percentage and the whole, we can find the part. For instance, what is 15% of 250? This is a straightforward calculation involving multiplying the percentage (as a decimal) by the whole.
-
Percentage Increase/Decrease: Calculating percentage changes (increases or decreases) requires understanding the difference between the initial and final values and expressing that difference as a percentage of the initial value. For instance, finding the percentage increase in sales from one year to the next.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: The key to mastering percentage calculations is consistent practice. Solve various problems to build your understanding and improve your speed.
-
Use Multiple Methods: Experiment with different methods to find the approach that suits you best. Understanding multiple approaches helps you develop a deeper understanding of the underlying concepts.
-
Break Down Complex Problems: For complex percentage problems, break them down into smaller, more manageable steps. This approach reduces errors and promotes clarity.
-
Utilize Online Resources: Numerous online resources, including calculators and tutorials, can help you improve your skills and check your work.
-
Understand the Context: Always pay attention to the context of the problem. Understanding the meaning of the numbers and what the question is asking is crucial for accurate calculation.
Conclusion: More Than Just Numbers
The seemingly simple question of "What percent of 120 is 15?" opens a door to a world of numerical understanding and practical application. Mastering percentage calculations isn't just about getting the right answer; it's about developing a crucial skill set applicable across various fields and everyday situations. By understanding the core concepts, exploring different methods, and practicing regularly, you can confidently navigate the world of percentages and leverage their power in your daily life and professional endeavors. Remember, the key to success lies in understanding the underlying principles and consistently applying them to various problems.
Latest Posts
Latest Posts
-
20 Out Of 28 As A Percentage
Apr 20, 2025
-
Can A Negative Number Be A Rational Number
Apr 20, 2025
-
How Many Cm In 71 Inches
Apr 20, 2025
-
What Is 5 5 In Meters
Apr 20, 2025
-
What Is The Percent Of 1 6
Apr 20, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 120 Is 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.