What Percent Of 15 Is 10
Kalali
Apr 10, 2025 · 5 min read
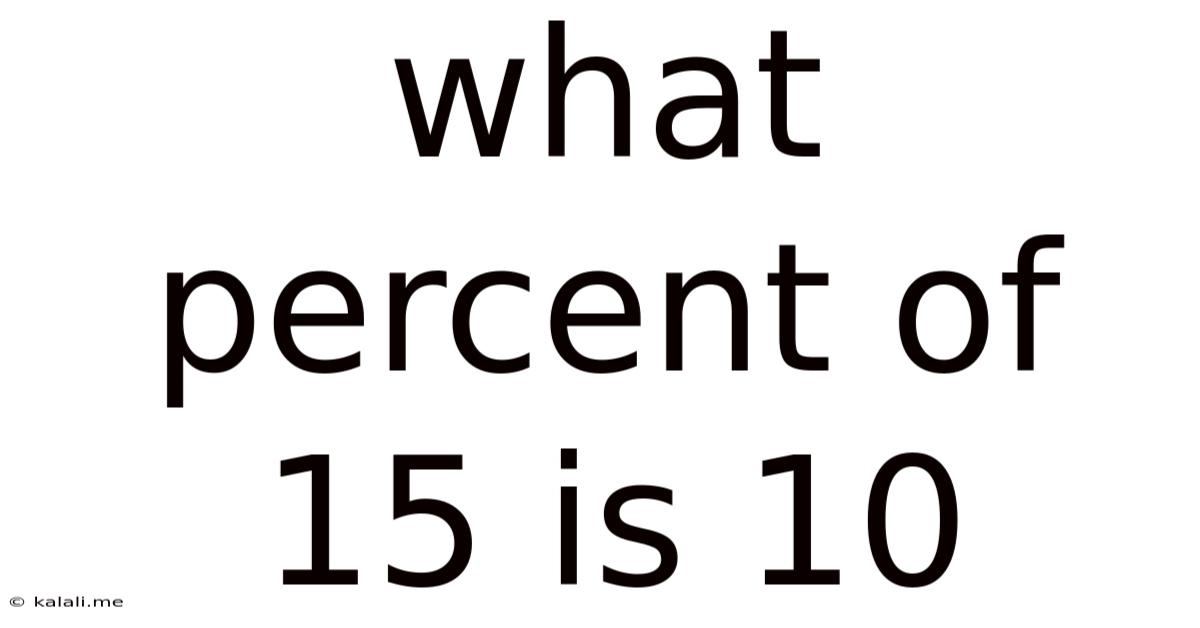
Table of Contents
What Percent of 15 is 10? Understanding Percentages and Their Applications
This seemingly simple question, "What percent of 15 is 10?", opens the door to a vast world of percentage calculations, their practical applications, and the underlying mathematical principles. While the answer itself is straightforward, understanding the how and why behind the calculation is crucial for navigating various scenarios in everyday life, from calculating discounts and taxes to understanding financial reports and statistical data. This article will delve deep into this question, exploring different methods of solving it, offering practical examples, and ultimately equipping you with a solid understanding of percentage calculations.
Meta Description: Learn how to calculate what percent of 15 is 10. This comprehensive guide covers various methods, real-world applications, and helps you master percentage calculations for everyday use.
Understanding the Fundamentals of Percentages
Before we tackle the specific problem, let's establish a solid foundation in percentages. A percentage is simply a fraction expressed as a number out of 100. The term "percent" originates from the Latin "per centum," meaning "out of a hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Percentages are used extensively to represent proportions, ratios, and changes in various contexts. They offer a standardized way to compare different quantities and express relative values. For example, a 10% increase in sales means that sales have increased by 10 units for every 100 units previously sold.
Method 1: Using the Formula
The most straightforward method to determine what percent of 15 is 10 involves using a simple formula:
(Part / Whole) x 100 = Percentage
In this case:
- Part: 10 (the value we want to express as a percentage)
- Whole: 15 (the total value)
Substituting these values into the formula:
(10 / 15) x 100 = Percentage
This simplifies to:
(2/3) x 100 ≈ 66.67%
Therefore, 10 is approximately 66.67% of 15.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. We can express the problem as:
10/15 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
10 x 100 = 15x
1000 = 15x
x = 1000 / 15
x ≈ 66.67%
This method confirms our previous result, demonstrating the consistency of different mathematical approaches.
Method 3: Using Decimal Equivalents
We can also solve this by first converting the fraction 10/15 to a decimal and then multiplying by 100 to express it as a percentage.
10/15 = 0.66666... (repeating decimal)
0.66666... x 100 ≈ 66.67%
This method highlights the relationship between decimals and percentages, showing how easily one can be converted into the other.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world scenarios. Here are a few examples:
-
Discounts and Sales: Retailers often advertise discounts as percentages. For example, a "20% off" sale means that you pay 80% of the original price. Knowing how to calculate percentages allows you to quickly determine the final price after a discount.
-
Taxes and Interest: Calculating taxes and interest rates involves percentages. Understanding these calculations is crucial for managing personal finances and making informed decisions about loans, investments, and other financial matters.
-
Financial Reporting: Companies use percentages extensively in financial reports to express key performance indicators (KPIs) such as profit margins, revenue growth, and market share. Analyzing these percentage changes helps investors and stakeholders understand the company's financial health and performance.
-
Statistical Analysis: Percentages are fundamental in statistical analysis, used to represent proportions, probabilities, and changes in data. For example, survey results are often presented as percentages to show the distribution of responses.
-
Scientific Calculations: In various scientific fields, percentages are employed to express concentrations, yields, and errors. Accurate percentage calculations are crucial for ensuring the reliability and validity of scientific research.
Beyond the Basics: More Complex Percentage Problems
While the problem "What percent of 15 is 10?" is relatively simple, the principles involved can be applied to more complex percentage calculations. For example:
- Finding the Whole: If you know the percentage and the part, you can calculate the whole. For instance, if 25% of a number is 5, you can set up the equation:
0.25x = 5
Solving for x (the whole number), you find x = 20.
-
Finding the Part: If you know the percentage and the whole, you can calculate the part. For example, if you want to find 30% of 80, you simply multiply 0.30 by 80, resulting in 24.
-
Percentage Change: Calculating the percentage change between two numbers involves finding the difference between the two numbers, dividing the difference by the original number, and multiplying by 100. For example, if a value increases from 50 to 60, the percentage change is calculated as:
((60 - 50) / 50) x 100 = 20%
This shows a 20% increase.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: The key to mastering percentage calculations is consistent practice. Solve various problems, starting with simple ones and gradually increasing the complexity.
-
Understand the Formula: Thoroughly understand the basic formula (Part / Whole) x 100 = Percentage and its variations.
-
Use Different Methods: Experiment with different methods – formulas, proportions, decimal equivalents – to find the approach that best suits your understanding and the problem at hand.
-
Check Your Answers: Always double-check your answers to ensure accuracy. You can often do this by using a different method to solve the same problem.
-
Utilize Online Calculators: While it's crucial to understand the underlying principles, online percentage calculators can be helpful for checking your work or solving complex problems quickly. However, always focus on understanding how the calculator arrives at its solution.
Conclusion: The Power of Percentages
The seemingly simple question, "What percent of 15 is 10?", serves as a gateway to a broader understanding of percentages and their widespread applications. From everyday shopping to complex financial analyses and scientific research, the ability to accurately calculate and interpret percentages is an invaluable skill. By mastering the fundamental concepts and practicing regularly, you can confidently navigate the world of percentages and use this knowledge to your advantage in numerous situations. Remember that while tools and calculators are helpful, a strong grasp of the underlying principles is paramount for true understanding and problem-solving success.
Latest Posts
Latest Posts
-
What Is 20 Ml In Ounces
Apr 18, 2025
-
Cuanto Es 45 Grados Centigrados En Fahrenheit
Apr 18, 2025
-
How Tall Is 52 In In Feet
Apr 18, 2025
-
What Factors Limit The Size Of A Cell
Apr 18, 2025
-
What Percentage Of 25 Is 8
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 15 Is 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.