What Percentage Of 25 Is 8
Kalali
Apr 18, 2025 · 5 min read
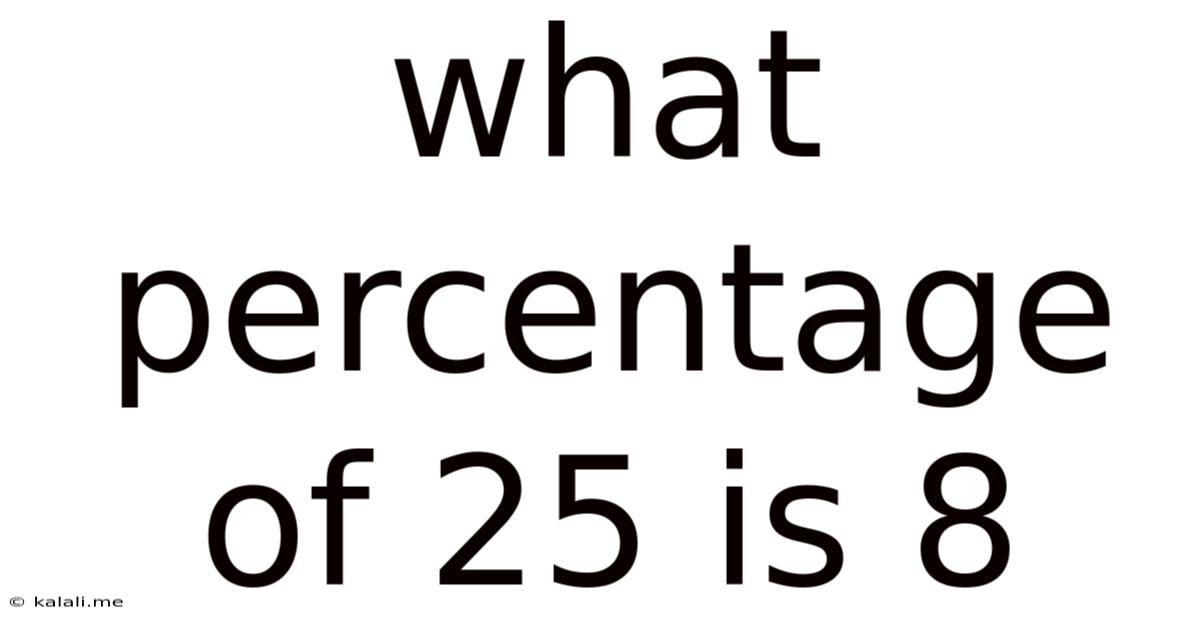
Table of Contents
What Percentage of 25 is 8? A Deep Dive into Percentage Calculations
Finding what percentage one number represents of another is a fundamental mathematical skill with wide-ranging applications in everyday life, from calculating discounts and tax rates to understanding statistical data and financial reports. This article explores how to determine what percentage 8 represents of 25, providing multiple methods and expanding on the underlying concepts to solidify your understanding of percentage calculations. We'll also look at real-world examples and explore how to apply this knowledge to similar problems. Understanding percentages is crucial for informed decision-making in numerous scenarios.
Meta Description: Learn how to calculate what percentage 8 is of 25 using various methods. This comprehensive guide covers the fundamental principles of percentage calculations and provides real-world examples. Master percentage calculations with ease!
Understanding Percentages: The Fundamentals
Before we delve into the specific calculation, let's refresh our understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The symbol "%" signifies "per hundred" or "out of 100." For example, 50% means 50 out of 100, which can also be represented as the fraction 50/100 or the decimal 0.5.
Understanding the relationship between fractions, decimals, and percentages is key to mastering percentage calculations. They are all different ways of expressing the same proportion. Converting between these forms is often necessary when working with percentages.
Method 1: Using the Formula
The most straightforward method for calculating the percentage one number represents of another is using the following formula:
(Part / Whole) * 100% = Percentage
In our case:
- Part: 8
- Whole: 25
Therefore, the calculation is:
(8 / 25) * 100% = 32%
Therefore, 8 is 32% of 25.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can set up a proportion to solve for the unknown percentage (x):
8/25 = x/100
To solve for x, we can cross-multiply:
25x = 800
Then, divide both sides by 25:
x = 800 / 25 = 32
Therefore, x = 32%, confirming that 8 is 32% of 25.
Method 3: Using Decimal Conversion
This method involves converting the fraction into a decimal and then multiplying by 100%. First, we divide the part by the whole:
8 / 25 = 0.32
Then, we multiply the decimal by 100% to convert it to a percentage:
0.32 * 100% = 32%
This again confirms that 8 is 32% of 25.
Real-World Applications: Putting Percentages to Work
Understanding percentage calculations is essential in various real-world situations. Here are a few examples:
-
Discounts: Imagine a store offering a 20% discount on an item originally priced at $25. To calculate the discount, you would find 20% of $25: (20/100) * $25 = $5. The discounted price would be $25 - $5 = $20. This involves understanding both percentage calculation and its application in subtractive scenarios.
-
Tax Calculation: Sales tax is commonly expressed as a percentage. If the sales tax in your area is 6%, and you buy an item costing $50, the tax amount would be (6/100) * $50 = $3. The total cost, including tax, would be $50 + $3 = $53. This shows how percentages are used in additive calculations.
-
Grade Calculation: Your grade on a test might be expressed as a percentage of the total possible points. If you scored 20 out of 25 points on a test, your percentage score is (20/25) * 100% = 80%. This application is vital for understanding academic performance and progress.
-
Financial Analysis: In finance, percentages are ubiquitous. Interest rates, returns on investments, and profit margins are all expressed as percentages. Analyzing financial statements often requires a thorough understanding of percentage changes and comparisons. For instance, comparing year-over-year growth requires the calculation of percentage increases or decreases in revenue, profit, or other key metrics.
-
Data Interpretation: Percentages are commonly used to represent data in charts, graphs, and reports. Understanding percentages helps in interpreting data effectively and making informed decisions based on the presented information. For example, understanding market share statistics often involves interpreting percentages.
Expanding on the Concept: More Complex Percentage Problems
While the example of finding what percentage 8 is of 25 is relatively straightforward, the principles can be applied to more complex scenarios. For instance, you might need to calculate a percentage increase or decrease, find the original value given a percentage change, or determine the percentage difference between two numbers.
Percentage Increase/Decrease: To calculate the percentage increase or decrease, you use the following formula:
[(New Value - Original Value) / Original Value] * 100%
For example, if the price of an item increased from $20 to $25, the percentage increase would be:
[(25 - 20) / 20] * 100% = 25%
Finding the Original Value: If you know the new value and the percentage change, you can work backward to find the original value. Let's say an item's price increased by 10% to $22. To find the original price, you can use algebra:
Original Value + 0.10 * Original Value = $22
1.10 * Original Value = $22
Original Value = $22 / 1.10 = $20
Tips for Mastering Percentage Calculations
-
Practice Regularly: The key to mastering percentage calculations is consistent practice. Work through various problems to build your understanding and confidence.
-
Use Multiple Methods: Familiarize yourself with different approaches, such as the formula method, the proportion method, and the decimal conversion method. Using multiple methods can help you check your answers and deepen your understanding of the underlying concepts.
-
Break Down Complex Problems: If you encounter a complex problem, break it down into smaller, more manageable steps. This will make the calculation process less daunting and reduce the chance of errors.
-
Use Online Calculators (Sparingly): While online calculators can be helpful for checking your work, it's crucial to understand the underlying principles. Over-reliance on calculators can hinder your ability to solve percentage problems independently.
-
Visual Aids: Diagrams and charts can be effective tools for visualizing percentage problems and making the calculations clearer.
Conclusion
Understanding what percentage 8 is of 25, and more broadly, mastering percentage calculations, is a fundamental skill with far-reaching implications in various aspects of life. By applying the methods outlined in this article and practicing regularly, you can confidently tackle percentage problems of varying complexities and apply this knowledge effectively in real-world situations. Remember, a strong grasp of percentages is a valuable asset for making informed decisions in academic, professional, and personal life. Through consistent practice and a solid understanding of the underlying principles, you can become proficient in solving percentage problems and confidently apply this essential skill across diverse contexts.
Latest Posts
Latest Posts
-
3 Out Of 13 As A Percentage
Apr 19, 2025
-
Which Statement Describes An Atomic Nucleus
Apr 19, 2025
-
What Is A Factor Of 56
Apr 19, 2025
-
Least Common Multiple Of 9 And 10
Apr 19, 2025
-
500 Ml Is How Many Cups Of Water
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 25 Is 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.