What Percent Of 15 Is 75
Kalali
Apr 13, 2025 · 4 min read
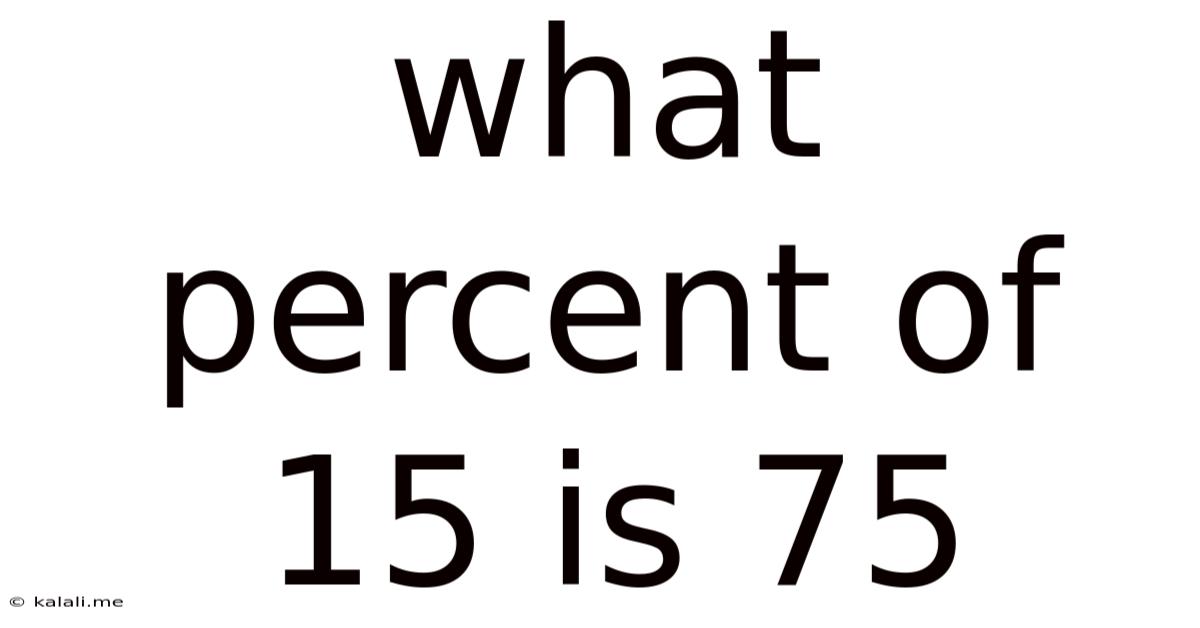
Table of Contents
What Percent of 15 is 75? Unraveling Percentage Calculations
This seemingly simple question, "What percent of 15 is 75?", opens the door to a deeper understanding of percentage calculations, a crucial skill in various aspects of life, from everyday budgeting to complex financial analysis. This article will not only answer the question directly but also explore the underlying concepts, provide multiple methods for solving similar problems, and offer practical applications to solidify your understanding. We'll delve into the core principles of percentages, explore different calculation approaches, and discuss common pitfalls to avoid.
Understanding Percentages: A Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred," indicating how many parts of a whole are represented. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Understanding this basic definition is key to mastering percentage calculations.
Method 1: Using the Formula
The most straightforward method to solve "What percent of 15 is 75?" involves using the percentage formula:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 75 (the value we're comparing)
- Whole: 15 (the total value)
Substituting these values into the formula, we get:
(75 / 15) x 100% = 500%
Therefore, 75 is 500% of 15. This result might seem counterintuitive at first glance, as percentages are often thought of as being less than or equal to 100%. However, percentages can exceed 100% when the part is larger than the whole, indicating a multiple of the whole.
Method 2: Setting up a Proportion
Another effective approach is setting up a proportion. This method is particularly useful for visualizing the relationship between the parts and the whole. We can set up the proportion as follows:
x/100 = 75/15
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
15x = 7500
Then, divide both sides by 15:
x = 500
Thus, we again arrive at the answer: 75 is 500% of 15.
Method 3: Using Decimal Conversion
This method leverages the conversion of percentages to decimals. First, we represent the unknown percentage as a decimal, 'x'. The equation then becomes:
x * 15 = 75
To solve for 'x', we divide both sides by 15:
x = 75 / 15 = 5
Since 'x' represents the decimal equivalent of the percentage, we convert it back to a percentage by multiplying by 100:
5 * 100% = 500%
Once again, the answer is 500%.
Interpreting the Result: Percentages Greater Than 100%
The result of 500% might appear unusual, but it's perfectly valid. Percentages exceeding 100% simply indicate that the "part" is more than the "whole." This often occurs in contexts involving growth, increases, or comparisons where one value surpasses another. For instance, if a company's profits increased from 15 million dollars to 75 million dollars, the increase would be 500% of the initial profit.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life and professional settings. Here are some examples:
- Finance: Calculating interest rates, loan repayments, profit margins, tax rates, and investment returns all rely heavily on percentage calculations. Understanding percentages is crucial for making informed financial decisions.
- Retail: Sales discounts, markups, and profit margins are expressed as percentages. Consumers need to understand percentages to compare prices and make informed purchasing decisions.
- Science: Many scientific calculations, particularly in statistics and data analysis, involve percentages. For example, expressing the concentration of a solution or the success rate of an experiment.
- Education: Grading systems, test scores, and progress reports frequently use percentages to represent academic performance.
- Everyday Life: Calculating tips, determining discounts, and understanding statistics in news reports all require an understanding of percentages.
Common Mistakes to Avoid
Several common errors can lead to inaccurate percentage calculations. These include:
- Incorrectly Identifying the Part and the Whole: Ensure you correctly identify the value representing the part and the value representing the whole. Misidentifying these values will lead to a wrong answer.
- Mathematical Errors: Carefully perform the arithmetic calculations (division and multiplication) to avoid errors. Using a calculator can minimize these mistakes.
- Misunderstanding Percentages Greater Than 100%: Remember that percentages can exceed 100% when the part is larger than the whole. Do not assume that all percentages must be between 0% and 100%.
- Incorrect Decimal to Percentage Conversion: When using the decimal conversion method, remember to multiply the decimal by 100% to obtain the final percentage.
Expanding Your Understanding: Further Exploration
To further strengthen your understanding of percentage calculations, consider exploring related concepts like:
- Percentage Change: Calculating the percentage increase or decrease between two values.
- Percentage Points: Understanding the difference between percentage change and percentage points.
- Compound Interest: Calculating interest that earns interest on previously accumulated interest.
Conclusion:
In conclusion, 75 is 500% of 15. This article has demonstrated several methods for solving this type of problem, highlighting the underlying principles of percentage calculations and providing practical applications. By understanding these principles and avoiding common mistakes, you can confidently tackle a wide range of percentage problems in various contexts, enhancing your problem-solving skills and improving your decision-making abilities. Remember, mastering percentage calculations is a valuable skill with far-reaching applications in numerous areas of life.
Latest Posts
Latest Posts
-
How Long Is 75 Inches In Feet
Apr 15, 2025
-
19 Is What Percent Of 76
Apr 15, 2025
-
The Following Sequence Has Terms That Decrease Exponentially
Apr 15, 2025
-
Cuantos Grados Centigrados Son 41 Fahrenheit
Apr 15, 2025
-
What Is 135 Out Of 150
Apr 15, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 15 Is 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.