What Percent Of 16 Is 6
Kalali
Apr 18, 2025 · 5 min read
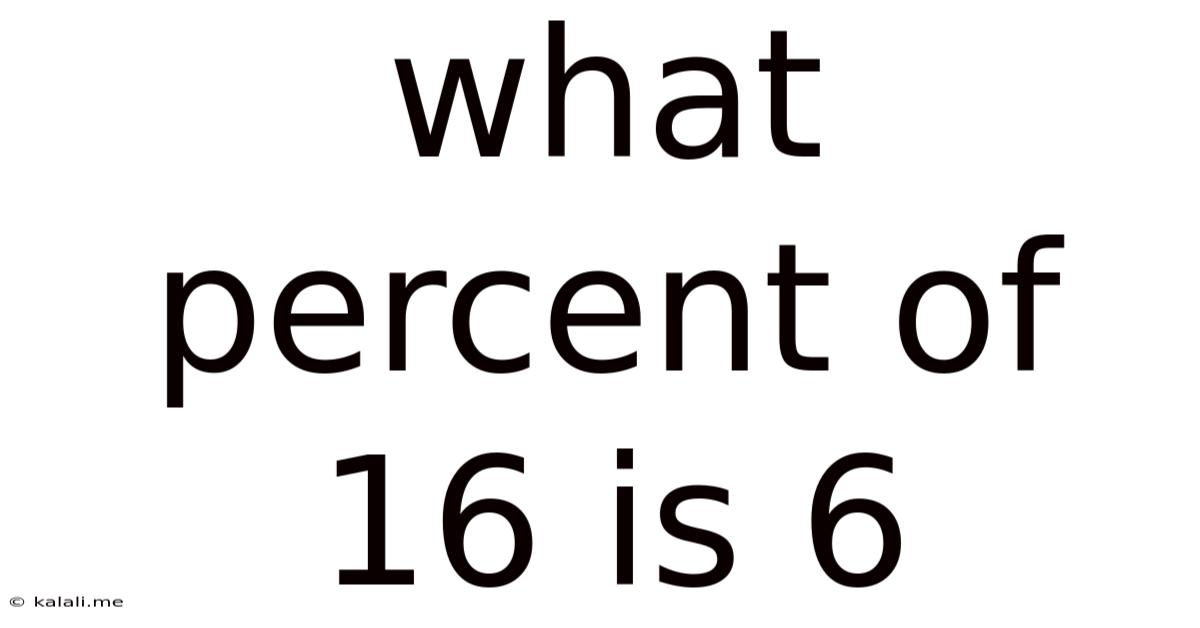
Table of Contents
What Percent of 16 is 6? A Comprehensive Guide to Percentage Calculations
This article delves into the seemingly simple question: "What percent of 16 is 6?" While the answer itself is straightforward, understanding the underlying mathematical concepts and exploring different approaches to solving percentage problems is crucial for various applications, from everyday budgeting to advanced statistical analysis. This guide will not only provide the solution but also equip you with the knowledge and tools to confidently tackle similar percentage calculations in the future. We’ll cover various methods, from simple arithmetic to using proportions and even algebraic equations. This comprehensive approach ensures a thorough understanding of percentage calculations, making you proficient in tackling a wide range of percentage-related problems.
Understanding Percentages: The Foundation
Before diving into the solution, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. This fundamental understanding forms the basis for all percentage calculations. Understanding this core concept is key to unlocking the world of percentages and applying them effectively in various contexts.
Method 1: Using the Formula
The most direct approach to solving "What percent of 16 is 6?" involves using the standard percentage formula:
(Part / Whole) * 100 = Percentage
In our problem:
- Part: 6 (the portion we're interested in)
- Whole: 16 (the total amount)
Substituting these values into the formula, we get:
(6 / 16) * 100 = Percentage
Calculating this gives us:
(0.375) * 100 = 37.5
Therefore, 6 is 37.5% of 16.
Method 2: Setting up a Proportion
Proportions offer another effective way to solve percentage problems. A proportion establishes an equivalence between two ratios. We can set up a proportion as follows:
x / 100 = 6 / 16
Here, 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
16x = 600
Then, divide both sides by 16:
x = 600 / 16 = 37.5
Again, we find that 6 is 37.5% of 16. This method demonstrates the power of proportions in solving percentage problems, providing an alternative approach to the direct formula method.
Method 3: Using Decimal Equivalents
This method leverages the relationship between decimals and percentages. First, we express the fraction 6/16 as a decimal:
6 / 16 = 0.375
To convert this decimal to a percentage, we simply multiply by 100:
0.375 * 100 = 37.5%
This approach highlights the seamless transition between decimals and percentages, offering a quick and efficient method for solving percentage problems. This method is particularly useful when dealing with calculator-based calculations, simplifying the process significantly.
Method 4: Algebraic Approach
A more formal approach involves setting up an algebraic equation. Let's represent the unknown percentage as 'x'. The problem can be expressed as:
x% of 16 = 6
Converting the percentage to a decimal, we get:
(x/100) * 16 = 6
Now, we solve for 'x':
16x = 600
x = 600 / 16
x = 37.5
Therefore, the answer remains 37.5%. This method demonstrates a more rigorous mathematical approach, ideal for understanding the underlying algebraic principles involved in percentage calculations.
Practical Applications of Percentage Calculations
Understanding percentage calculations is not just an academic exercise; it has widespread practical applications in various aspects of life. Here are a few examples:
-
Financial Calculations: Calculating interest rates, discounts, taxes, profit margins, and tips all involve percentage calculations. Understanding these calculations is crucial for effective financial planning and decision-making. From calculating simple interest on savings accounts to understanding complex compound interest, percentages are essential tools.
-
Data Analysis: Percentages are frequently used to represent proportions and trends in data. Analyzing survey results, market research, and scientific studies often involves expressing data as percentages to facilitate comparison and interpretation. Visualizing data using percentage charts and graphs is crucial for data communication.
-
Everyday Life: Calculating discounts in stores, determining the tip at a restaurant, or understanding the nutritional content of food products all involve percentage calculations. This highlights the prevalence of percentage calculations in everyday life, making it a crucial skill to acquire.
-
Scientific and Engineering Applications: Percentages are fundamental in scientific and engineering fields for expressing error margins, efficiency rates, and various other measurements. The application spans diverse fields, demonstrating its significance across scientific disciplines.
Advanced Percentage Problems and Techniques
While the problem "What percent of 16 is 6?" is relatively straightforward, more complex percentage problems may involve multiple steps or require more advanced techniques. For example, calculating percentage increase or decrease, finding the original value after a percentage change, or dealing with compound percentages requires a deeper understanding of the underlying principles. These advanced scenarios highlight the importance of grasping the fundamentals to effectively tackle complex percentage-related problems.
Conclusion:
Solving "What percent of 16 is 6?" provides a foundation for understanding percentage calculations. The answer, 37.5%, can be derived through various methods, each offering a unique perspective on the problem-solving process. Whether you use the basic formula, proportions, decimal equivalents, or an algebraic approach, the core concept remains the same: expressing a part as a fraction of a whole and then converting it to a percentage. This understanding extends far beyond simple calculations, impacting various aspects of our lives from personal finance to professional applications. Mastering these techniques empowers you to tackle a wide range of percentage-based problems with confidence and precision. The ability to confidently perform these calculations is a valuable skill, making you well-equipped for both personal and professional scenarios that involve percentages.
Latest Posts
Latest Posts
-
What Is A Factor Of 56
Apr 19, 2025
-
Least Common Multiple Of 9 And 10
Apr 19, 2025
-
500 Ml Is How Many Cups Of Water
Apr 19, 2025
-
15 Of What Number Is 6
Apr 19, 2025
-
What Percent Of 15 Is 11
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 16 Is 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.