What Percent Of 15 Is 11
Kalali
Apr 19, 2025 · 5 min read
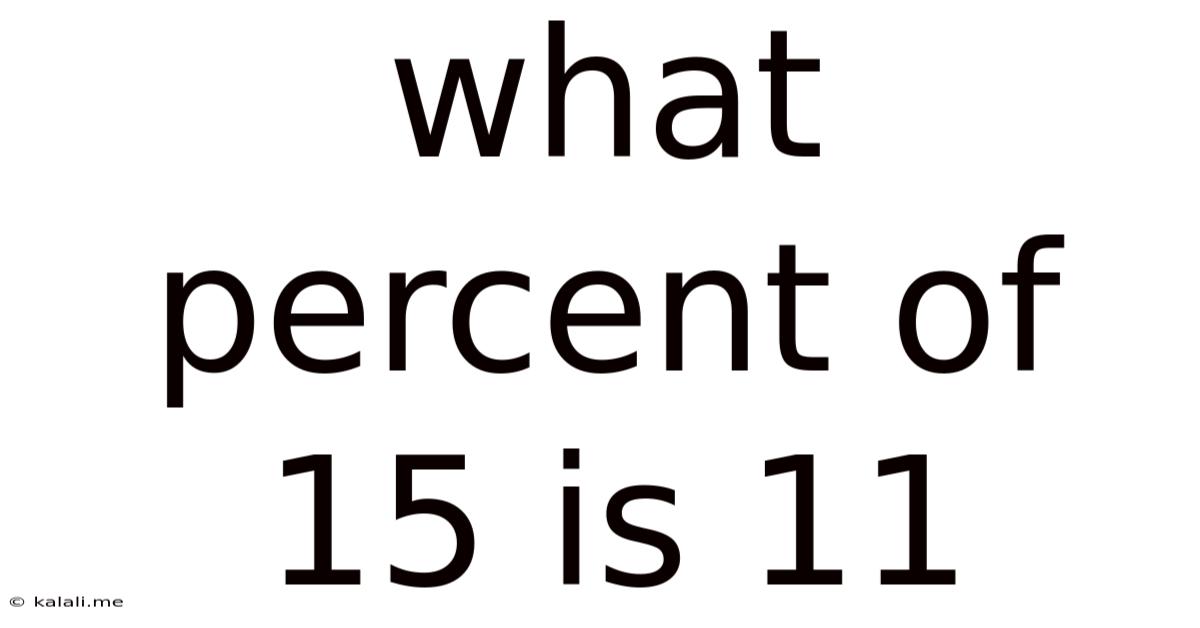
Table of Contents
What Percent of 15 is 11? A Deep Dive into Percentage Calculations
This seemingly simple question, "What percent of 15 is 11?", unlocks a world of practical applications in everyday life, from calculating discounts and sales tax to understanding financial reports and analyzing statistical data. While the answer might seem straightforward, understanding the underlying principles and various methods for solving this type of problem is crucial for anyone seeking to improve their mathematical proficiency and data interpretation skills. This article will explore different approaches to solving this problem, discuss the concepts of percentages, ratios, and proportions, and illustrate how these concepts can be applied in various real-world scenarios.
Understanding Percentages: The Foundation
A percentage is a way of expressing a number as a fraction of 100. It represents a proportion or a part of a whole. The symbol "%" represents "per cent," meaning "out of one hundred." Understanding this fundamental concept is essential for tackling percentage calculations efficiently. For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Method 1: Using the Percentage Formula
The most direct way to solve "What percent of 15 is 11?" is by using the standard percentage formula:
(Part / Whole) x 100 = Percentage
In this case:
- Part: 11 (the number representing the portion of the whole)
- Whole: 15 (the total amount or the base value)
Substituting these values into the formula, we get:
(11 / 15) x 100 = Percentage
Calculating this:
(0.7333...) x 100 ≈ 73.33%
Therefore, 11 is approximately 73.33% of 15. The "..." indicates that the decimal continues infinitely, but for practical purposes, rounding to two decimal places is usually sufficient.
Method 2: Using Proportions
Proportions offer another effective method for solving percentage problems. A proportion is an equation stating that two ratios are equal. We can set up a proportion to solve "What percent of 15 is 11?" as follows:
x/100 = 11/15
Here, 'x' represents the percentage we want to find. To solve for 'x', we can cross-multiply:
15x = 1100
Now, divide both sides by 15:
x = 1100 / 15
x ≈ 73.33
Therefore, once again, we find that 11 is approximately 73.33% of 15.
Method 3: Using Decimals
This method involves converting the percentage into a decimal and then solving the equation. We can represent "x% of 15 is 11" as:
(x/100) * 15 = 11
Now, solve for x:
x/100 = 11/15
x = (11/15) * 100
x ≈ 73.33
This method reinforces the relationship between percentages, fractions, and decimals, providing a flexible approach to percentage calculations.
Real-World Applications: Beyond the Classroom
Understanding percentage calculations transcends the confines of mathematics textbooks; it's a vital skill applicable across numerous real-world scenarios. Consider these examples:
1. Sales and Discounts: Imagine a store offers a discount on an item originally priced at $15. If the discounted price is $11, using the methods described above, we can calculate that the discount is approximately 73.33%. This calculation helps consumers determine the value of a sale.
2. Financial Analysis: Percentage calculations are fundamental to interpreting financial statements. For example, understanding the percentage change in a company's revenue or profit from one year to the next is crucial for evaluating its financial performance. Analyzing percentage changes helps investors assess growth trends and make informed investment decisions. This also applies to personal finance: tracking percentage changes in savings, investments, or expenses allows for better financial management.
3. Statistical Analysis: Percentages are extensively used in statistical analysis to represent proportions within datasets. For example, researchers might report that 75% of participants in a study showed a particular response. This percentage summarizes the distribution of responses and provides a concise way to interpret data.
4. Grade Calculations: In education, percentages are used to calculate grades and scores. A student obtaining 11 marks out of a total of 15 marks would receive a grade equivalent to approximately 73.33%.
5. Tax Calculations: Sales tax, income tax, and other taxes are often expressed as percentages. Understanding these percentages is vital for accurately calculating tax liabilities and making informed financial decisions.
6. Tip Calculations: When calculating a tip at a restaurant, people often use percentages. For example, a 15% tip on a $10 meal is calculated by finding 15% of $10.
7. Surveys and Polls: Results from surveys and polls are often presented as percentages to represent the proportion of respondents who selected a particular option. This allows for easier understanding and comparison of different perspectives.
Beyond the Basics: Advanced Applications
While the basic percentage formula serves as a robust foundation, more advanced applications might involve dealing with percentage increases or decreases, compound interest calculations, and complex statistical analyses. These advanced techniques require a deeper understanding of mathematical principles and may involve using more sophisticated formulas and tools.
Percentage Increase/Decrease: Calculating percentage increases or decreases requires considering the change in value relative to the original value. The formula for percentage increase is:
[(New Value - Original Value) / Original Value] x 100
The formula for percentage decrease is the same, but the result will be negative.
Compound Interest: Compound interest involves earning interest not only on the principal amount but also on accumulated interest. This calculation involves exponential growth and requires more complex formulas.
Error Analysis: In scientific and engineering contexts, percentage error analysis helps quantify the accuracy and precision of measurements. It involves comparing the measured value to the true value and expressing the difference as a percentage.
Conclusion: Mastering Percentages for a Data-Driven World
The seemingly simple question of "What percent of 15 is 11?" serves as a gateway to understanding the broader world of percentage calculations and their widespread applications. Whether it's calculating discounts, analyzing financial data, interpreting research findings, or understanding everyday financial transactions, mastering percentage calculations is an indispensable skill in today's data-driven world. By understanding the different methods of solving percentage problems and applying them to real-world situations, individuals can develop valuable analytical skills and enhance their decision-making capabilities across various domains. The ability to accurately interpret and utilize percentages is no longer just a mathematical skill; it's a crucial life skill.
Latest Posts
Latest Posts
-
What Is 8 12 As A Percentage
Apr 22, 2025
-
2 Out Of 3 As A Percentage
Apr 22, 2025
-
How Many Liters In 64 Ounces
Apr 22, 2025
-
Cuanto Son 70 Grados Fahrenheit En Centigrados
Apr 22, 2025
-
Common Multiples Of 5 And 15
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 15 Is 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.