What Percent Of 18 Is 3
Kalali
Apr 25, 2025 · 4 min read
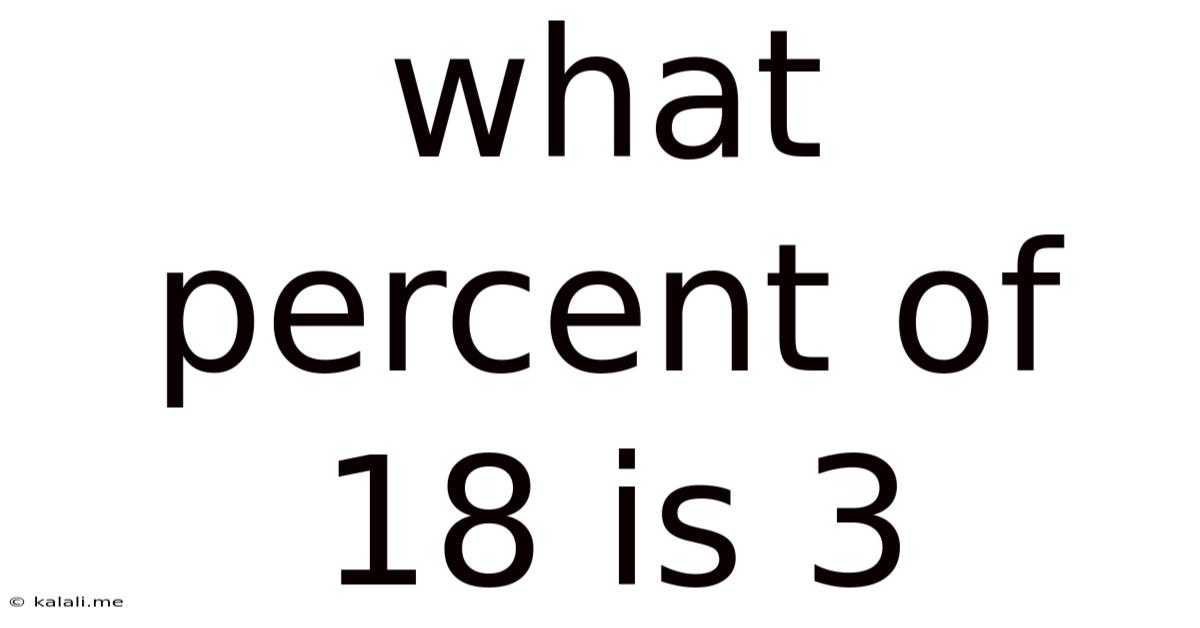
Table of Contents
What Percent of 18 is 3? A Comprehensive Guide to Percentage Calculations
This article delves into the seemingly simple question: "What percent of 18 is 3?" While the answer might seem immediately obvious to some, understanding the underlying principles and different methods for solving percentage problems is crucial for a wide range of applications, from everyday budgeting to complex financial analysis. This guide provides a step-by-step breakdown of the solution, explores various approaches, and offers valuable insights into percentage calculations in general. We'll also examine related concepts and provide practice problems to solidify your understanding.
Understanding Percentages:
A percentage is a fraction or ratio expressed as a number out of 100. It represents a portion of a whole. The symbol "%" signifies "percent" or "out of 100." For example, 50% means 50 out of 100, which simplifies to 1/2 or 0.5. Understanding this fundamental concept is key to solving percentage problems effectively. Percentage calculations are used extensively in many fields including:
- Finance: Calculating interest rates, discounts, taxes, and profit margins.
- Statistics: Analyzing data and presenting findings in a clear and concise manner.
- Science: Expressing concentrations, probabilities, and experimental results.
- Everyday Life: Determining tips, sales discounts, and understanding proportions.
Method 1: Using Proportions
This method utilizes the concept of ratios and proportions to solve for the unknown percentage. We can set up a proportion as follows:
- Part/Whole = Percentage/100
In our problem, the "part" is 3, the "whole" is 18, and the "percentage" is what we need to find (let's represent it as 'x'). This gives us the proportion:
3/18 = x/100
To solve for x, we cross-multiply:
3 * 100 = 18 * x
300 = 18x
Now, divide both sides by 18:
x = 300 / 18
x = 16.67 (approximately)
Therefore, 3 is approximately 16.67% of 18.
Method 2: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
-
Form the fraction: Express the problem as a fraction: 3/18
-
Simplify the fraction (if possible): We can simplify 3/18 by dividing both the numerator and the denominator by their greatest common divisor, which is 3:
3/18 = 1/6
-
Convert the fraction to a decimal: Divide the numerator (1) by the denominator (6):
1 ÷ 6 ≈ 0.1667
-
Convert the decimal to a percentage: Multiply the decimal by 100:
0.1667 * 100 = 16.67%
Therefore, using this method, we again find that 3 is approximately 16.67% of 18.
Method 3: Using the Percentage Formula
The basic percentage formula is:
(Part / Whole) * 100 = Percentage
Substituting the values from our problem:
(3 / 18) * 100 = Percentage
(1/6) * 100 = Percentage
0.1667 * 100 ≈ 16.67%
This method directly applies the fundamental percentage formula and yields the same result: 3 is approximately 16.67% of 18.
Understanding the Approximation:
Notice that in all methods, we arrive at an approximate answer of 16.67%. This is because the fraction 1/6 is a repeating decimal (0.166666...). We round the decimal to a reasonable number of significant figures for practical purposes. In many contexts, rounding to two decimal places (16.67%) is sufficient. However, in situations requiring greater precision, you might use more decimal places or express the answer as a fraction (1/6).
Practical Applications:
Understanding percentage calculations is essential for various real-world situations. Here are a few examples:
-
Sales Discounts: A store offers a 20% discount on an item originally priced at $30. To calculate the discount, you would find 20% of $30, which is (20/100) * $30 = $6. The discounted price would be $30 - $6 = $24.
-
Tax Calculations: If the sales tax is 8%, and you buy an item for $50, the tax amount is (8/100) * $50 = $4. The total cost would be $50 + $4 = $54.
-
Tip Calculation: A common practice is to tip 15% to 20% in restaurants. If your bill is $75, a 15% tip would be (15/100) * $75 = $11.25.
-
Grade Calculation: If you scored 27 out of 30 on a test, your percentage score would be (27/30) * 100 ≈ 90%.
-
Financial Investments: Calculating interest earned on savings accounts, returns on investments, and understanding loan repayments all involve percentage calculations.
Practice Problems:
Try solving these problems using the methods discussed above:
- What percent of 25 is 5?
- What percent of 100 is 35?
- 12 is what percent of 48?
- What is 30% of 80?
- If you receive a 10% discount on a $65 item, what is the final price?
Conclusion:
Determining what percent of 18 is 3 involves fundamental percentage calculations. This article has demonstrated three reliable methods to solve such problems: using proportions, decimal conversion, and the direct application of the percentage formula. Mastering these methods empowers you to tackle various percentage-related challenges in various fields, enhancing your problem-solving abilities in everyday life and professional endeavors. Remember to choose the method that best suits your understanding and the specific context of the problem. Consistent practice will solidify your understanding and increase your confidence in performing accurate percentage calculations.
Latest Posts
Latest Posts
-
How Many Sides A Quadrilateral Have
Apr 25, 2025
-
Whats 3 To The Power Of 3
Apr 25, 2025
-
Least Common Multiple Of 9 And 5
Apr 25, 2025
-
What Pattern Do You Notive When Square Numbers
Apr 25, 2025
-
How Many Lines Of Symmetry Does Circle Have
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 18 Is 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.