What Percent Of 20 Is 7
Kalali
Mar 26, 2025 · 4 min read
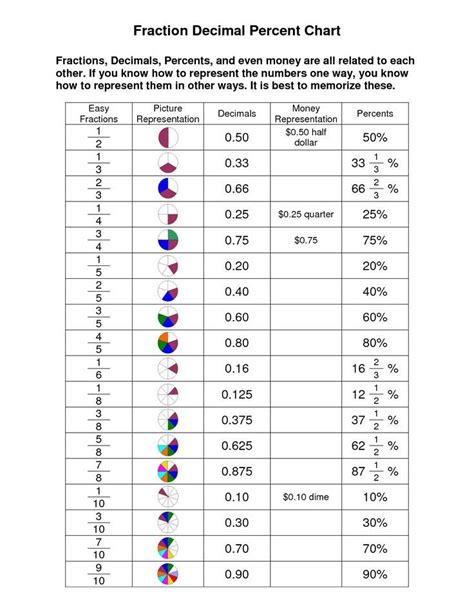
Table of Contents
What Percent of 20 is 7? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analyses. This article delves into the question, "What percent of 20 is 7?", providing a detailed explanation of the solution, exploring different methods, and extending the understanding to more complex percentage problems. We’ll cover the basics, delve into the practical applications, and offer tips for mastering percentage calculations.
Understanding Percentages
Before tackling the specific problem, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "per hundred" or "out of 100." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Method 1: Using the Proportion Method
The proportion method is a classic and intuitive way to solve percentage problems. We can set up a proportion to represent the problem "What percent of 20 is 7?" as follows:
x/100 = 7/20
Where:
- x represents the unknown percentage we're trying to find.
- 100 represents the total percentage (100%).
- 7 represents the part we're comparing to the whole (20).
- 20 represents the whole amount.
To solve for x, we cross-multiply:
20x = 700
Then, divide both sides by 20:
x = 700/20 = 35
Therefore, 7 is 35% of 20.
Method 2: Using the Decimal Method
This method involves converting the percentage problem into a decimal equation. We can express "What percent of 20 is 7?" as:
x * 20 = 7
Here, 'x' represents the decimal equivalent of the percentage we need to find. To solve for x, we divide both sides by 20:
x = 7/20 = 0.35
To convert this decimal to a percentage, we multiply by 100:
x = 0.35 * 100 = 35%
Again, we arrive at the solution: 7 is 35% of 20.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the process. Here's how you'd typically solve it:
- Divide: Divide 7 by 20 (7 ÷ 20 = 0.35).
- Multiply: Multiply the result by 100 (0.35 × 100 = 35).
The calculator directly gives you the answer: 35%.
Extending the Understanding: Variations and Applications
The fundamental principle of calculating percentages remains the same, even when the problem changes slightly. Let's consider some variations:
Finding the Whole Amount
What if we knew that 35% of a number is 7, and we want to find the whole number? We can set up the equation as:
0.35 * x = 7
Solving for x:
x = 7 / 0.35 = 20
This confirms that 7 is 35% of 20.
Finding the Part
What if we want to find what 25% of 20 is? We can use the same methods:
Method 1 (Proportion):
x/20 = 25/100
x = (25 * 20) / 100 = 5
Method 2 (Decimal):
0.25 * 20 = 5
Therefore, 25% of 20 is 5.
Real-World Applications
Percentage calculations are pervasive in our daily lives. Here are some examples:
- Sales and Discounts: Calculating discounts on items during sales. If a shirt is 20% off its original price of $50, the discount is 0.20 * $50 = $10.
- Taxes: Determining sales tax or income tax amounts.
- Tips and Gratuities: Calculating appropriate tips in restaurants.
- Finance: Calculating interest on loans or investments. Compound interest calculations involve repeated percentage calculations.
- Statistics: Analyzing data sets, interpreting survey results, and expressing probabilities.
- Science: Representing experimental data, calculating concentrations of solutions.
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The more you practice, the more comfortable and efficient you'll become. Try solving various percentage problems from different contexts.
- Understand the Fundamentals: A solid grasp of fractions and decimals is crucial for efficient percentage calculations.
- Use Multiple Methods: Employing different methods helps to cross-check your answers and build a deeper understanding.
- Visual Aids: Diagrams and charts can help to visualize percentage problems, making them easier to comprehend.
- Online Resources: Several online calculators and tutorials can assist in learning and practicing percentage calculations.
Conclusion: Beyond the Basics
This article has explored the problem "What percent of 20 is 7?" in detail, offering multiple methods of solution and emphasizing the broader applications of percentage calculations. Mastering percentage calculations is a valuable skill that empowers you to tackle a wide range of problems, both in your personal life and professional endeavors. Remember that consistent practice and a solid understanding of the underlying principles are key to becoming proficient in this important mathematical skill. The ability to confidently and accurately work with percentages opens doors to understanding and navigating the quantitative world around us more effectively. By mastering these techniques, you equip yourself with a crucial tool for problem-solving and decision-making in many aspects of life.
Latest Posts
Latest Posts
-
Is Ductility A Physical Or Chemical Property
Mar 30, 2025
-
Lowest Common Factor Of 3 And 4
Mar 30, 2025
-
How Much Is 1 4 Cup In Ounces
Mar 30, 2025
-
What Percentage Is 1 In 6
Mar 30, 2025
-
What Is The Thickness Of The Outer Core
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 20 Is 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
