What Percent Of 25 Is 8
Kalali
Apr 11, 2025 · 5 min read
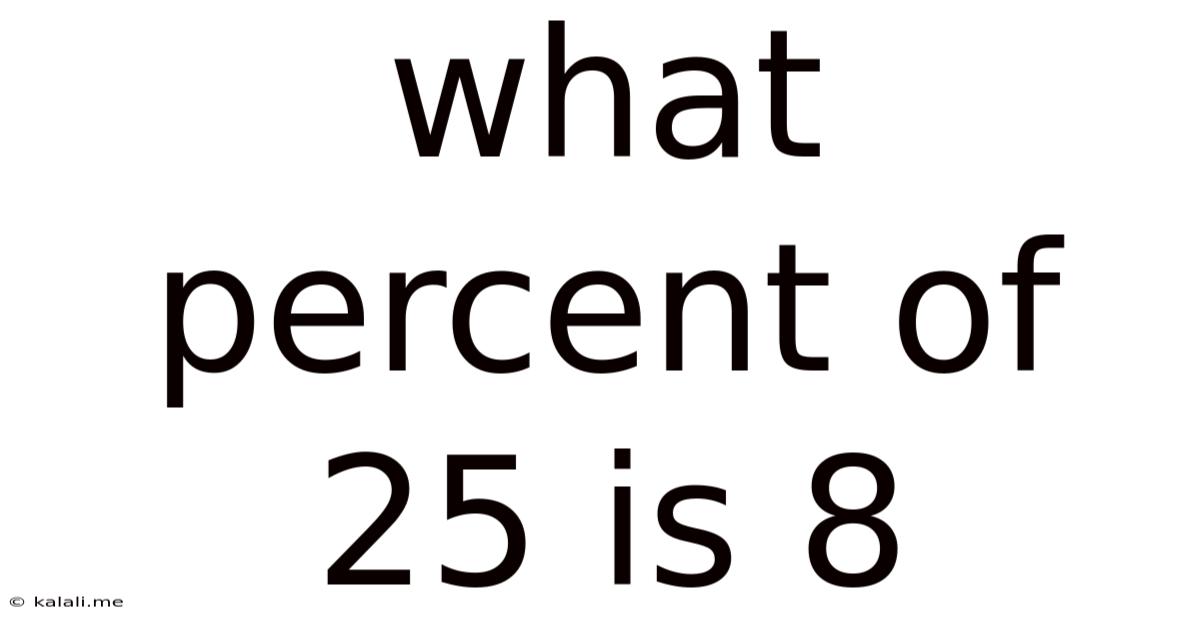
Table of Contents
What Percent of 25 is 8? A Deep Dive into Percentage Calculations
This seemingly simple question – "What percent of 25 is 8?" – opens the door to a broader understanding of percentage calculations, their applications, and the various methods used to solve them. While a quick calculation might provide the immediate answer, exploring the underlying principles enhances comprehension and allows for tackling more complex percentage problems. This article will not only answer the question directly but will also delve into different approaches, provide real-world examples, and explore the importance of percentage calculations in various fields.
Meta Description: Learn how to calculate percentages, understand the different methods for solving percentage problems, and discover real-world applications of percentage calculations. We'll answer the question: What percent of 25 is 8? and much more!
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" ("per centum" in Latin). Understanding this foundational concept is crucial to solving any percentage problem. It represents a proportion or ratio, offering a standardized way to compare different quantities. For instance, 50% means 50 out of 100, which simplifies to 1/2 or 0.5.
Method 1: The Proportion Method
This method utilizes the concept of ratios and proportions to solve percentage problems. We can set up a proportion to solve "What percent of 25 is 8?" as follows:
- Part/Whole = Percentage/100
In this case:
- Part: 8 (the number we're interested in finding the percentage of)
- Whole: 25 (the total amount)
- Percentage: x (this is what we need to find)
Substituting these values into the proportion, we get:
8/25 = x/100
To solve for x, we cross-multiply:
25x = 800
Then, we divide both sides by 25:
x = 32
Therefore, 8 is 32% of 25.
Method 2: The Decimal Method
This method involves converting the percentage to a decimal and then using multiplication. First, we represent "what percent of 25 is 8" as an equation:
x * 25 = 8
To solve for x (the percentage expressed as a decimal), we divide both sides by 25:
x = 8/25
This gives us x = 0.32. To convert this decimal to a percentage, we multiply by 100:
0.32 * 100 = 32%
Again, we arrive at the answer: 8 is 32% of 25.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the process. The specific steps may vary depending on the calculator model, but generally, you can input the following:
(8 ÷ 25) * 100 = 32
This directly calculates the percentage. This method is efficient for quick calculations but understanding the underlying principles remains crucial for complex problems.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of life, including:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and returns on investments. For instance, understanding the percentage change in stock prices is essential for investors. A 10% increase in a stock’s value represents a significant change in its worth.
-
Retail: Determining sale prices, calculating markups, and analyzing sales figures. Retailers frequently use percentages to advertise discounts ("20% off!"), and understanding markups is critical to their profitability.
-
Science: Expressing experimental results, calculating error margins, and analyzing statistical data. Scientific research often involves comparing data sets, and percentages provide a standardized way to do so. For instance, reporting the percentage of participants who responded favorably to a new treatment is standard practice in medical research.
-
Education: Calculating grades, assessing student performance, and tracking progress. Grade point averages (GPAs) and standardized test scores are often expressed as percentages, providing a concise summary of academic achievement.
-
Everyday Life: Tip calculations in restaurants, figuring out sales tax, determining the percentage of completion on a project, or even understanding nutritional information on food labels (percentage of daily value for nutrients).
Solving More Complex Percentage Problems
While the initial problem was relatively straightforward, percentage calculations can become more complex. Here are some examples:
-
Finding the whole: If 20% of a number is 15, what is the number? This involves setting up an equation: 0.20 * x = 15, and solving for x.
-
Finding the part: What is 15% of 60? This is a direct calculation: 0.15 * 60 = 9.
-
Percentage change: If a price increased from $50 to $60, what is the percentage increase? This involves calculating the difference ($10), dividing it by the original price ($50), and multiplying by 100. The result is a 20% increase.
Tips for Mastering Percentage Calculations
-
Practice regularly: The more you practice, the more comfortable you will become with different types of percentage problems.
-
Understand the concepts: Don't just memorize formulas; understand the underlying principles of ratios, proportions, and decimals.
-
Use different methods: Experiment with the proportion method, the decimal method, and using a calculator to find the most efficient approach for you.
-
Check your work: Always double-check your calculations to ensure accuracy.
-
Break down complex problems: If you encounter a complex problem, break it down into smaller, more manageable steps.
Conclusion
The seemingly simple question, "What percent of 25 is 8?", provides a gateway to understanding the versatile world of percentage calculations. By mastering different methods and grasping the underlying principles, you can confidently tackle various percentage problems encountered in academic, professional, and everyday life. The ability to perform percentage calculations efficiently and accurately is a valuable skill applicable across numerous disciplines, making it a fundamental aspect of numerical literacy. Remember to practice regularly and explore different methods to solidify your understanding and build confidence in solving these crucial calculations.
Latest Posts
Latest Posts
-
108 Is What Percent Of 200
Apr 18, 2025
-
How Much Is 50 Feet In Meters
Apr 18, 2025
-
What Is 12 Degrees In Celsius
Apr 18, 2025
-
How Much Is 800 Ml In Cups
Apr 18, 2025
-
61 Inches To Feet And Inches
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 25 Is 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.