What Percent Of 30 Is 75
Kalali
Apr 22, 2025 · 5 min read
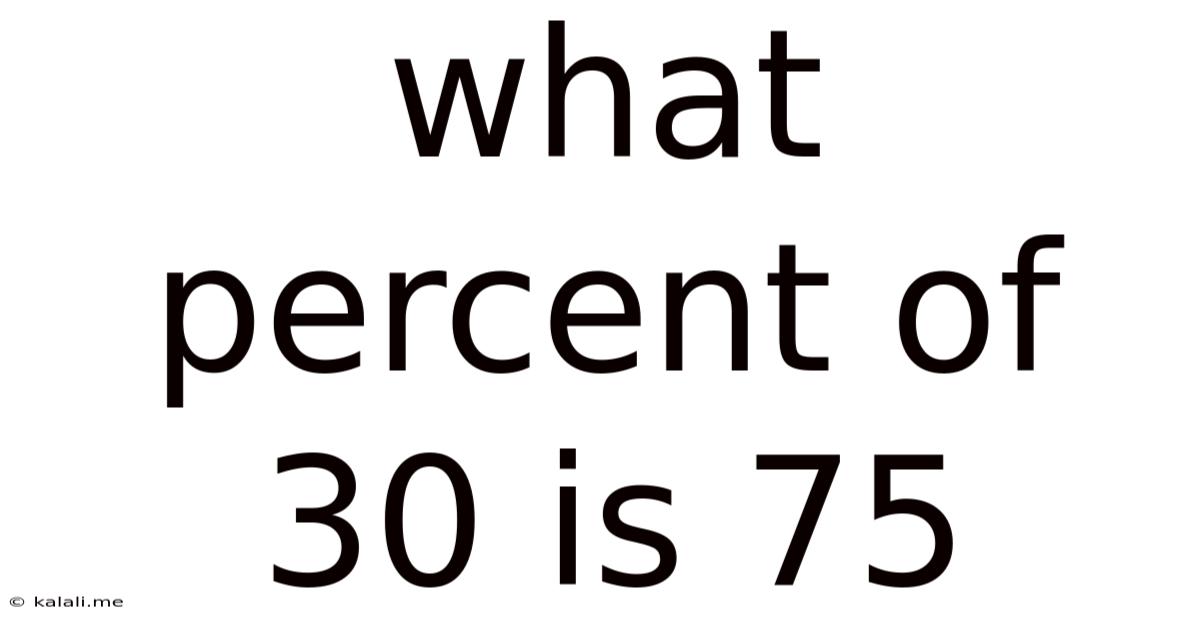
Table of Contents
What Percent of 30 is 75? Unpacking Percentage Calculations and Their Applications
This seemingly simple question, "What percent of 30 is 75?", opens the door to a broader understanding of percentage calculations, their practical applications, and how to approach similar problems with confidence. While the answer itself is straightforward, the underlying mathematical concepts and real-world uses are far-reaching. This article will delve into the solution, explore different methods for calculating percentages, and illustrate their importance across various fields.
Meta Description: Discover how to calculate what percent of 30 is 75. This comprehensive guide explores percentage calculations, different solution methods, and real-world applications, equipping you with the skills to tackle similar problems with ease.
Understanding the Basics of Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Percentages are used extensively to represent proportions, changes, and rates in various contexts. For example, a 10% discount means a reduction of 10 units for every 100 units. Understanding percentages is crucial for everyday life, from calculating sales tax to interpreting financial reports.
Method 1: Using the Formula
The most direct way to solve "What percent of 30 is 75?" is by using the standard percentage formula:
(Part / Whole) * 100 = Percentage
In this case:
- Part: 75 (the number we want to express as a percentage of 30)
- Whole: 30 (the total or base number)
Substituting the values into the formula:
(75 / 30) * 100 = 250%
Therefore, 75 is 250% of 30. This result indicates that 75 is more than 30; it's two and a half times larger.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as follows:
x/100 = 75/30
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
30x = 7500
Then, divide both sides by 30:
x = 250
Therefore, once again, we find that 75 is 250% of 30. This method provides a clear visual representation of the relationship between the parts and the whole.
Method 3: Using Decimal Equivalents
Percentages can also be expressed as decimals. To do this, divide the percentage by 100. For example, 25% is equal to 0.25. We can use this method to solve our problem in a slightly different way:
Let's represent "x percent of 30 is 75" as an equation:
x/100 * 30 = 75
First, simplify the equation:
0.3x = 75
Then, divide both sides by 0.3:
x = 75 / 0.3 = 250
Again, the answer confirms that 75 is 250% of 30. This approach highlights the relationship between percentages and their decimal equivalents.
Real-World Applications of Percentage Calculations
Percentage calculations are indispensable across numerous fields:
-
Finance: Calculating interest rates, loan repayments, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentage changes is essential for analyzing market trends and making informed financial decisions. For instance, understanding compound interest necessitates a strong grasp of percentage growth over time. Analyzing stock market performance invariably involves percentage changes.
-
Business: Businesses use percentages for sales tax calculations, profit margin analysis, discount offers, and market share evaluation. Calculating the percentage of sales attributed to a particular product line helps in strategic decision-making. Marketing campaigns often focus on percentage-based metrics like conversion rates and customer acquisition costs.
-
Science: In scientific research, percentages are used to express experimental results, error margins, and statistical significance. Data analysis often involves calculating percentages to summarize and interpret findings. For instance, expressing the percentage of a population exhibiting a particular characteristic is standard practice in epidemiological studies.
-
Education: Grading systems, performance evaluations, and scholarship awards often rely on percentages. Understanding the percentage of correct answers on a test is crucial for students to assess their comprehension.
-
Everyday Life: Sales discounts, tax rates, tips at restaurants, and even nutritional information on food labels all involve percentages. Being proficient in percentage calculations is crucial for making informed consumer choices and managing personal finances. Even understanding weather forecasts often involves percentages related to the chance of precipitation.
Beyond the Basics: More Complex Percentage Problems
While the "What percent of 30 is 75?" problem is relatively simple, more complex scenarios can arise. For example:
-
Percentage Increase/Decrease: Calculating the percentage change between two values requires understanding the difference between the initial and final values, expressing this difference as a fraction of the initial value, and then multiplying by 100 to express it as a percentage. This is commonly used to track changes in prices, populations, or other measurable quantities.
-
Percentage Points vs. Percentages: It's important to distinguish between a percentage point change and a percentage change. A percentage point change refers to the absolute difference between two percentages, while a percentage change expresses the relative difference as a percentage of the initial value. For example, a change from 10% to 20% is a 10-percentage point increase, but a 100% percentage increase.
-
Compounding Percentages: When percentages are applied repeatedly (such as with compound interest), the calculations become more complex. Understanding the concept of compounding is essential for accurately predicting future values.
-
Multiple Percentages: Calculating the effect of applying multiple percentages sequentially (for instance, successive discounts) requires careful attention to the order of operations.
Mastering Percentage Calculations: Tips and Practice
To become proficient in percentage calculations, consistent practice is key. Here are some tips:
-
Understand the Fundamentals: Ensure you have a solid grasp of the basic concepts of fractions, decimals, and ratios. These are the building blocks of percentage calculations.
-
Practice Regularly: Work through various problems, starting with simple examples and gradually increasing the complexity.
-
Use Multiple Methods: Try different approaches to solving percentage problems to develop a deeper understanding of the underlying principles.
-
Check Your Answers: Always double-check your calculations to ensure accuracy. Using a calculator can be helpful, but understanding the underlying math is crucial.
-
Seek Help When Needed: Don't hesitate to consult textbooks, online resources, or tutors if you encounter difficulties.
In conclusion, the seemingly straightforward question "What percent of 30 is 75?" provides a springboard to explore the multifaceted world of percentage calculations. Understanding these calculations is not just about solving mathematical problems; it's about developing a crucial skill applicable to numerous aspects of life, from personal finance to professional pursuits. By mastering these concepts and practicing regularly, you can confidently tackle any percentage-related challenge that comes your way.
Latest Posts
Latest Posts
-
14 Of 20 As A Percentage
Apr 22, 2025
-
What Is 30 Out Of 41
Apr 22, 2025
-
What Is The Reciprocal Of 6
Apr 22, 2025
-
At What Temperature Does Blood Boil
Apr 22, 2025
-
What Is 8 12 As A Percentage
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 30 Is 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.