What Percent Of 4 Is 15
Kalali
Apr 09, 2025 · 5 min read
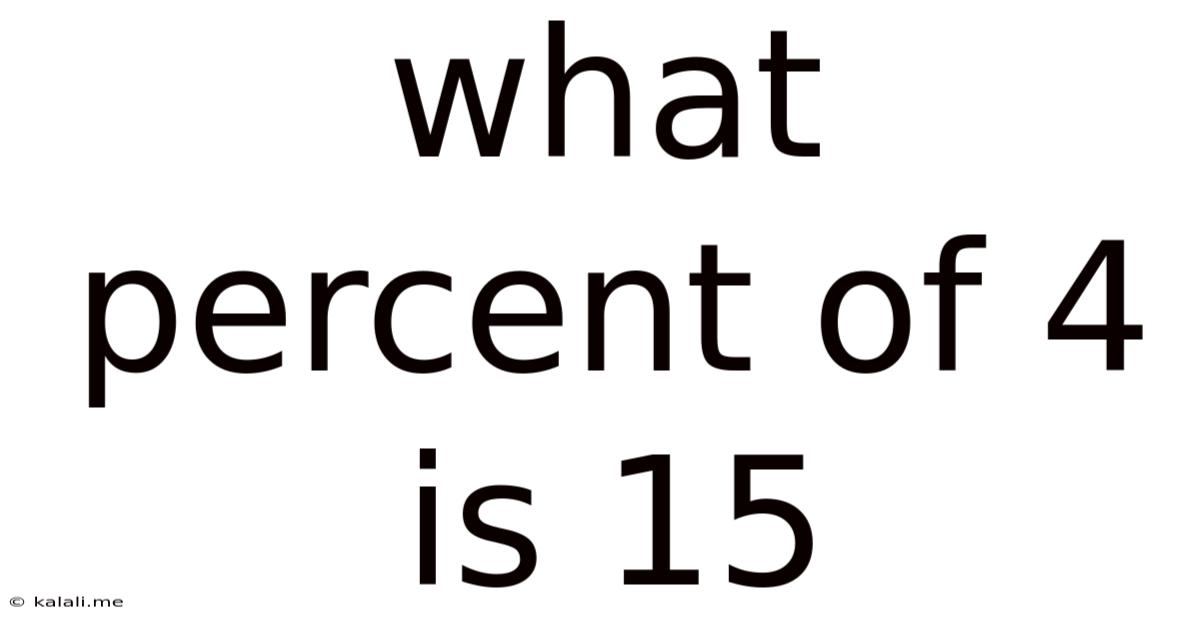
Table of Contents
What Percent of 4 is 15? Understanding Percentages and Proportions
This seemingly simple question, "What percent of 4 is 15?", delves into the fundamental concepts of percentages and proportions. At first glance, it might seem counterintuitive – how can a part (15) be larger than the whole (4)? This scenario highlights the importance of understanding the underlying mathematical principles and applying them correctly. This article will explore the solution, explain the methodology, and discuss related concepts to build a comprehensive understanding of percentages and their applications. We'll also look at how to solve similar problems and even tackle more complex scenarios involving percentages.
Meta Description: Discover how to calculate what percent of 4 is 15. This comprehensive guide breaks down the process, explains the underlying concepts of percentages and proportions, and provides practical examples to enhance your understanding. Learn to solve similar problems and apply this knowledge to various real-world situations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100". For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Percentages are used extensively in various fields, including finance, statistics, and everyday life. Understanding percentages is crucial for interpreting data, making informed decisions, and solving practical problems.
Setting up the Proportion
To determine what percent of 4 is 15, we need to set up a proportion. A proportion is a statement that two ratios are equal. In this case, we can set up the proportion as follows:
- x/100 = 15/4
Where:
- x represents the percentage we're trying to find.
- 100 represents the total percentage (the whole).
- 15 represents the part.
- 4 represents the whole.
This proportion states that the ratio of the unknown percentage (x) to 100 is equal to the ratio of the part (15) to the whole (4).
Solving the Proportion
To solve for x, we can cross-multiply:
- 4x = 15 * 100
- 4x = 1500
Now, divide both sides of the equation by 4:
- x = 1500 / 4
- x = 375
Therefore, 15 is 375% of 4.
Interpreting the Result
The result, 375%, indicates that 15 is three and three-quarters times larger than 4. This is perfectly valid mathematically; percentages aren't limited to values between 0 and 100. A percentage greater than 100 simply means that the part is larger than the whole. This often occurs in scenarios involving growth, increase, or comparisons where the initial value is used as a baseline.
Practical Applications and Real-World Examples
Understanding how to calculate percentages beyond 100% has practical applications in various situations:
-
Financial Growth: Imagine investing $4 and seeing your investment grow to $15. Calculating the percentage increase would give you 375%, showcasing significant growth.
-
Sales and Marketing: A company might experience a 375% increase in sales compared to the previous year. This represents a dramatic improvement and would likely require further analysis to understand the contributing factors.
-
Data Analysis: In statistical analysis, percentages exceeding 100% might be encountered when comparing different data sets or measuring changes over time.
-
Scientific Measurements: Various scientific measurements and experiments might result in values exceeding the initial baseline, requiring the calculation of percentages greater than 100%.
-
Recipe Scaling: Imagine a recipe calling for 4 cups of flour but you want to make a significantly larger batch. If you want to use 15 cups of flour, you'd be using 375% of the original recipe's flour quantity.
Solving Similar Problems: A Step-by-Step Guide
Let's look at how to solve similar problems involving percentages:
Problem 1: What percent of 8 is 20?
- Set up the proportion: x/100 = 20/8
- Cross-multiply: 8x = 2000
- Solve for x: x = 2000 / 8 = 250
- Answer: 20 is 250% of 8.
Problem 2: What percent of 12 is 6?
- Set up the proportion: x/100 = 6/12
- Cross-multiply: 12x = 600
- Solve for x: x = 600 / 12 = 50
- Answer: 6 is 50% of 12.
Problem 3: What percent of 25 is 75?
- Set up the proportion: x/100 = 75/25
- Cross-multiply: 25x = 7500
- Solve for x: x = 7500 / 25 = 300
- Answer: 75 is 300% of 25.
Advanced Concepts and Further Exploration
While the basic concept of percentages is relatively straightforward, more advanced concepts build upon this foundation:
-
Percentage Change: Calculating the percentage increase or decrease between two values. This involves finding the difference between the two values, dividing by the original value, and multiplying by 100.
-
Compound Interest: Calculating interest on both the principal amount and accumulated interest over time. This involves repeated applications of percentage calculations.
-
Percentage Points: These are used when comparing percentage changes. For example, a change from 20% to 25% is a 5 percentage point increase, but a 25% increase relative to the initial 20%.
-
Statistical Significance: In statistics, percentages are used to represent the probability or likelihood of an event occurring.
-
Data Visualization: Percentages are frequently used in charts and graphs to represent proportions and trends in data.
Conclusion: Mastering Percentages for Real-World Success
Understanding percentages is a crucial skill applicable to numerous aspects of life. The question "What percent of 4 is 15?" serves as an excellent example of how percentages can extend beyond the 0-100 range, representing situations where a part is larger than the whole. By mastering the fundamentals of proportions and applying them systematically, you can confidently tackle various percentage-related problems, enabling you to interpret data, make informed decisions, and succeed in various academic and professional endeavors. Remember to always carefully define your "whole" and "part" when setting up your proportion to ensure accurate calculations.
Latest Posts
Latest Posts
-
What Is 18 20 As A Percent
Apr 17, 2025
-
11 As A Percentage Of 25
Apr 17, 2025
-
7 Is What Percent Of 8
Apr 17, 2025
-
2 1 4 As An Improper Fraction
Apr 17, 2025
-
65 Cm Equals How Many Inches
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 4 Is 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.