What Percent Of 40 Is 70
Kalali
Apr 13, 2025 · 5 min read
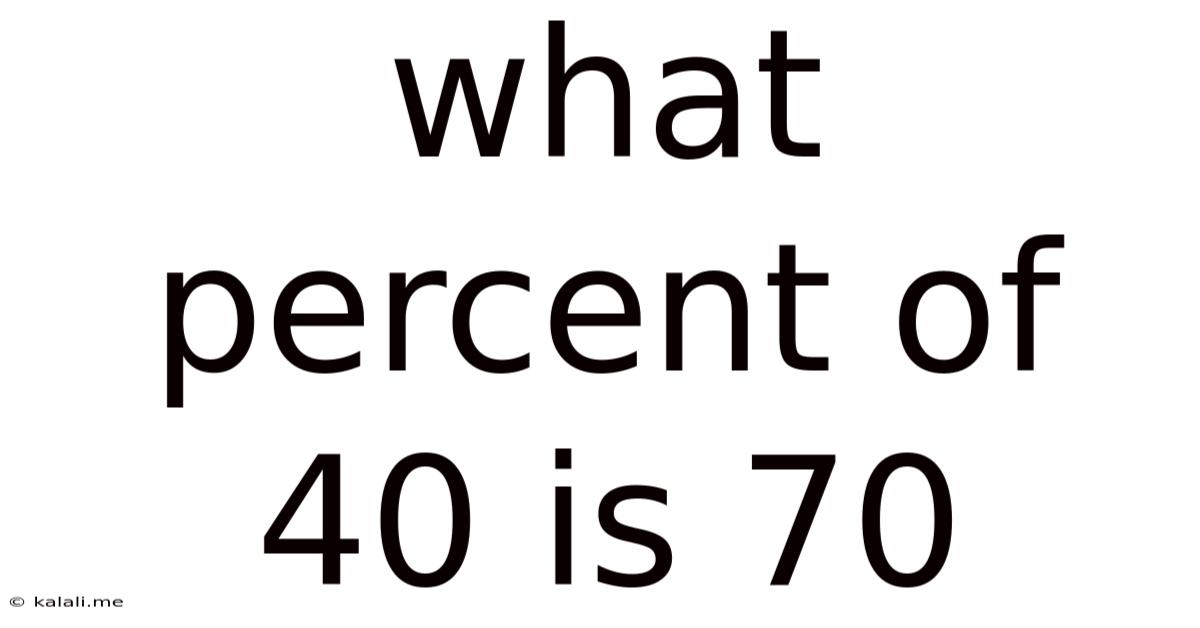
Table of Contents
What Percent of 40 is 70? Unpacking the Concept of Percentages and Their Applications
This seemingly simple question, "What percent of 40 is 70?", delves into a fundamental concept in mathematics: percentages. Understanding percentages is crucial not only for academic success but also for navigating everyday life, from calculating discounts and taxes to understanding financial reports and statistical data. This article will not only answer the question directly but also explore the underlying principles, various methods of calculation, and practical applications of percentage calculations. We'll also delve into common percentage-related problems and offer strategies for solving them effectively. The meta description is: Learn how to calculate percentages, understand the concept of "what percent of 40 is 70," and explore practical applications in everyday life and beyond.
Understanding Percentages: A Foundation
A percentage is simply a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred" or "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. This seemingly simple concept forms the basis of many mathematical operations and real-world calculations.
Understanding percentages is about understanding the relationship between a part and a whole. The whole is typically represented as 100%, and any portion of that whole is represented as a percentage less than 100%. If you have a pie and eat half of it, you have consumed 50% of the pie. If you eat a quarter of it, you have consumed 25%.
Calculating "What Percent of 40 is 70?"
Now, let's tackle the core question: What percent of 40 is 70? This question might seem counterintuitive at first glance, as 70 is larger than 40. This indicates that the percentage will be greater than 100%. This is perfectly valid; percentages can and often do exceed 100%. Here are a few different methods to solve this:
Method 1: Using Proportions
This method involves setting up a proportion, which is an equation showing two equal ratios. We can represent the problem as:
x/100 = 70/40
Here, 'x' represents the percentage we're trying to find. To solve for x, we cross-multiply:
40x = 7000
Then, divide both sides by 40:
x = 175
Therefore, 70 is 175% of 40.
Method 2: Using Decimal Conversion
This method converts the fraction to a decimal and then multiplies by 100 to express it as a percentage.
First, represent the problem as a fraction: 70/40
Next, divide 70 by 40: 70 ÷ 40 = 1.75
Finally, multiply the decimal by 100 to convert it to a percentage: 1.75 * 100 = 175%
So again, we find that 70 is 175% of 40.
Method 3: Formulaic Approach
A more direct formulaic approach can be used:
Percentage = (Part / Whole) * 100
In this case, the 'part' is 70, and the 'whole' is 40. Substituting these values into the formula:
Percentage = (70 / 40) * 100 = 175%
This confirms our previous calculations.
Practical Applications of Percentage Calculations
The ability to calculate percentages is vital in numerous real-world situations. Here are a few examples:
-
Calculating Discounts: If a store offers a 20% discount on an item priced at $100, the discount amount is (20/100) * $100 = $20, and the final price is $100 - $20 = $80.
-
Determining Taxes: If a sales tax is 6%, the tax amount on a $50 purchase is (6/100) * $50 = $3. The total cost is $50 + $3 = $53.
-
Understanding Financial Reports: Percentages are extensively used in financial statements to show growth rates, profit margins, and other key financial metrics. For example, a company's revenue growth might be expressed as a percentage increase or decrease compared to the previous year.
-
Analyzing Statistical Data: Percentages are essential for interpreting and presenting statistical data. For instance, survey results are often expressed as percentages to show the proportion of respondents who chose a particular answer.
-
Calculating Interest: Compound interest calculations heavily rely on percentage calculations to determine the amount of interest earned or paid over time.
Solving More Complex Percentage Problems
While the initial problem was relatively straightforward, many percentage problems can be more intricate. Let's look at some examples and strategies for solving them:
Problem 1: Finding the Whole when given a Part and Percentage
-
Example: 25% of a number is 15. What is the number?
-
Solution: Let the number be 'x'. We can set up an equation: 0.25x = 15. Solving for x, we get x = 15 / 0.25 = 60.
Problem 2: Finding the Percentage Increase or Decrease
-
Example: A price increased from $50 to $60. What is the percentage increase?
-
Solution: The increase is $60 - $50 = $10. The percentage increase is ($10 / $50) * 100 = 20%.
Problem 3: Dealing with Multiple Percentage Changes
-
Example: A price is increased by 10% and then decreased by 10%. Is the final price the same as the original?
-
Solution: No, the final price will be slightly lower than the original. Let's say the original price is $100. A 10% increase makes it $110. A 10% decrease from $110 is $110 - ($110 * 0.10) = $99.
This demonstrates that percentage changes are not always additive or subtractive in a straightforward manner.
Tips and Tricks for Mastering Percentage Calculations
-
Practice Regularly: The best way to master percentage calculations is through consistent practice. Solve a variety of problems to build your understanding and confidence.
-
Utilize Online Calculators and Tools: Many online calculators and tools can assist in percentage calculations, especially for more complex problems. Use these tools to verify your calculations and identify any errors.
-
Understand the Underlying Concepts: Don't just memorize formulas; strive to grasp the fundamental principles of percentages, ratios, and fractions.
-
Break Down Complex Problems: If a problem seems overwhelming, break it down into smaller, manageable parts.
Conclusion
The question "What percent of 40 is 70?" serves as an excellent entry point into the world of percentage calculations. Understanding percentages is a crucial skill with wide-ranging applications in various aspects of life. By mastering the methods described in this article, you'll be well-equipped to tackle a wide range of percentage-related problems and confidently apply this fundamental mathematical concept to real-world situations. Remember to practice regularly and focus on understanding the underlying concepts to truly master this essential skill. The ability to quickly and accurately calculate percentages will undoubtedly enhance your problem-solving capabilities and give you a significant advantage in many academic and professional contexts.
Latest Posts
Latest Posts
-
Name Four Groups Of Organic Compounds Found In Living Things
Apr 14, 2025
-
Least Common Multiple Of 7 And 12
Apr 14, 2025
-
What Percent Of 80 Is 12
Apr 14, 2025
-
Cuanto Es 100 Ml En Oz
Apr 14, 2025
-
Whats The Lcm Of 8 And 9
Apr 14, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 40 Is 70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.