What Percent Of 80 Is 12
Kalali
Apr 14, 2025 · 6 min read
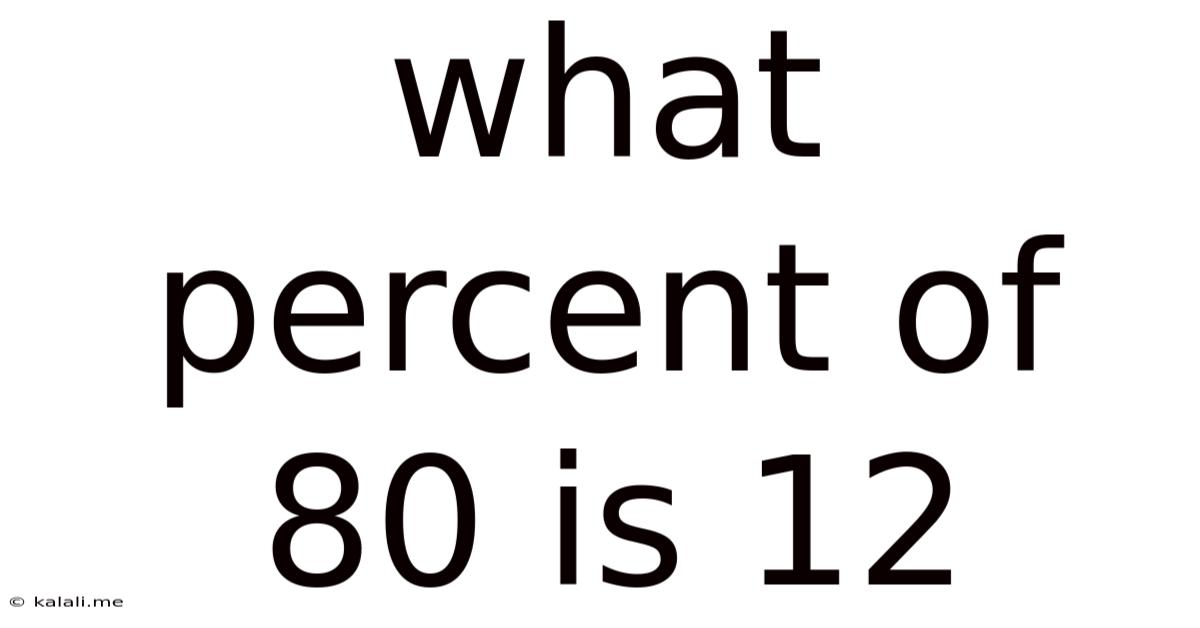
Table of Contents
What Percent of 80 is 12? A Deep Dive into Percentage Calculations
Finding out what percentage 12 represents of 80 might seem like a simple arithmetic problem. However, understanding the underlying principles and exploring different methods of solving it not only provides the answer but also builds a stronger foundation in percentage calculations, a skill crucial in various aspects of life, from finance to data analysis. This article will thoroughly explore this seemingly simple question, offering multiple approaches, practical applications, and tips for mastering percentage calculations. This includes exploring the concept of percentages, various methods of calculation, and real-world examples to solidify your understanding.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to determine what percent of 80 is 12. We explore multiple methods, real-world applications, and offer tips for mastering percentage calculations.
Understanding Percentages
Before diving into the calculation, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent" or "out of 100." For instance, 50% means 50 out of 100, which is equivalent to 50/100 or 1/2. Percentages are a fundamental tool for representing proportions, comparing quantities, and understanding changes in values. They are ubiquitous in everyday life, appearing in discounts, interest rates, tax calculations, and statistical data.
Method 1: Using the Percentage Formula
The most straightforward way to solve "What percent of 80 is 12?" is to use the basic percentage formula:
(Part / Whole) x 100 = Percentage
In this case:
- Part: 12 (the value we want to express as a percentage)
- Whole: 80 (the total value)
Applying the formula:
(12 / 80) x 100 = 15%
Therefore, 12 is 15% of 80.
Method 2: Setting up a Proportion
Another approach involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can express the problem as:
12/80 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
12 * 100 = 80 * x
1200 = 80x
x = 1200 / 80
x = 15
Therefore, 12 is 15% of 80. This method emphasizes the proportional relationship between the parts and the whole.
Method 3: Using Decimal Equivalents
Percentages can also be expressed as decimals. To find the decimal equivalent of a percentage, divide the percentage by 100. For example, 15% is equivalent to 0.15 (15/100). We can use this approach to solve the problem:
Let 'x' be the percentage. Then:
x/100 * 80 = 12
Solving for x:
x * 80 = 1200
x = 1200 / 80
x = 15
Therefore, the answer is again 15%. This method highlights the interchangeability between percentages and decimals, showcasing a crucial aspect of numerical fluency.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in various real-world scenarios. Here are a few examples:
- Finance: Calculating interest rates on loans, savings accounts, or investments. Understanding discounts and sales tax on purchases. Analyzing financial statements and budgets. Determining profit margins.
- Sales and Marketing: Calculating sales growth, conversion rates, and customer acquisition costs. Analyzing market share and conducting market research. Setting pricing strategies based on profit margins and competitor analysis.
- Data Analysis: Representing data visually using charts and graphs that include percentages. Analyzing survey results and statistical data. Calculating proportions and distributions in datasets. Understanding statistical significance and error margins.
- Everyday Life: Calculating tips in restaurants, splitting bills among friends, understanding discounts in stores, and comparing prices of different products. Calculating the percentage of completion for tasks and projects.
These examples demonstrate the wide applicability of percentage calculations in practical situations, from personal finance to professional settings.
Tips for Mastering Percentage Calculations
Here are some tips to help improve your proficiency in percentage calculations:
- Practice Regularly: Consistent practice is key to mastering any mathematical skill. Work through various percentage problems, starting with simple ones and gradually increasing the complexity.
- Understand the Concepts: Ensure you have a solid grasp of the fundamental concepts behind percentages, including fractions, decimals, and ratios.
- Use Multiple Methods: Familiarize yourself with different methods for solving percentage problems, such as the formula method, proportion method, and decimal method. This will broaden your understanding and allow you to choose the most efficient method for each problem.
- Check Your Work: Always check your answers to ensure accuracy. You can do this by working backward or using a different method to solve the same problem.
- Utilize Online Resources: Many online resources, including calculators and tutorials, can help you practice and learn more about percentage calculations. These resources can provide additional practice problems and explanations.
- Break Down Complex Problems: If faced with a complex problem involving percentages, break it down into smaller, more manageable parts. This will make the problem easier to solve and reduce the risk of errors.
These strategies can significantly enhance your skills in handling percentage calculations and improve your confidence in tackling more challenging problems.
Expanding the Understanding: Variations on the Problem
While we've focused on "What percent of 80 is 12?", let's explore variations to deepen our understanding:
- What is 15% of 80? This is the reverse of our original problem. Using the formula (Percentage/100) * Whole = Part, we get (15/100) * 80 = 12. This reinforces the inverse relationship between finding a percentage and finding a part given a percentage.
- 12 is 15% of what number? This variation requires solving for the "whole." We can set up the equation: 0.15 * x = 12. Solving for x, we find x = 80. This highlights the flexibility of percentage calculations and their adaptability to different problem types.
- What is the percentage increase from 68 to 80? This involves calculating the percentage change. First, find the difference (80-68=12). Then, divide the difference by the original number (12/68) and multiply by 100 to get the percentage increase (approximately 17.6%). This demonstrates the application of percentages in analyzing changes in quantities.
These examples showcase how the fundamental principles of percentage calculations can be applied to a wider range of problems, illustrating the versatility and importance of mastering this skill.
Conclusion: Mastering the Art of Percentages
Determining what percent of 80 is 12 is more than just a simple calculation; it’s a gateway to understanding the broader world of percentages and their applications. By mastering the different methods presented—from the straightforward formula to the proportional approach and the use of decimal equivalents—you equip yourself with a powerful tool applicable across various fields. Remember to practice regularly, utilize different methods, and break down complex problems into smaller, manageable parts. With consistent effort and a deeper understanding of the underlying concepts, you'll confidently navigate the world of percentages and their numerous applications in your personal and professional life. The ability to quickly and accurately calculate percentages is a skill that will undoubtedly serve you well.
Latest Posts
Latest Posts
-
What Percent Of 75 Is 33
Apr 15, 2025
-
60 Is What Percent Of 25
Apr 15, 2025
-
How Many Vertices Does A Circle Have
Apr 15, 2025
-
How Many Meters Is 220 Feet
Apr 15, 2025
-
Cuanto Es 3 Pies En Centimetros
Apr 15, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 80 Is 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.