What Percent Of 48 Is 36
Kalali
Apr 16, 2025 · 4 min read
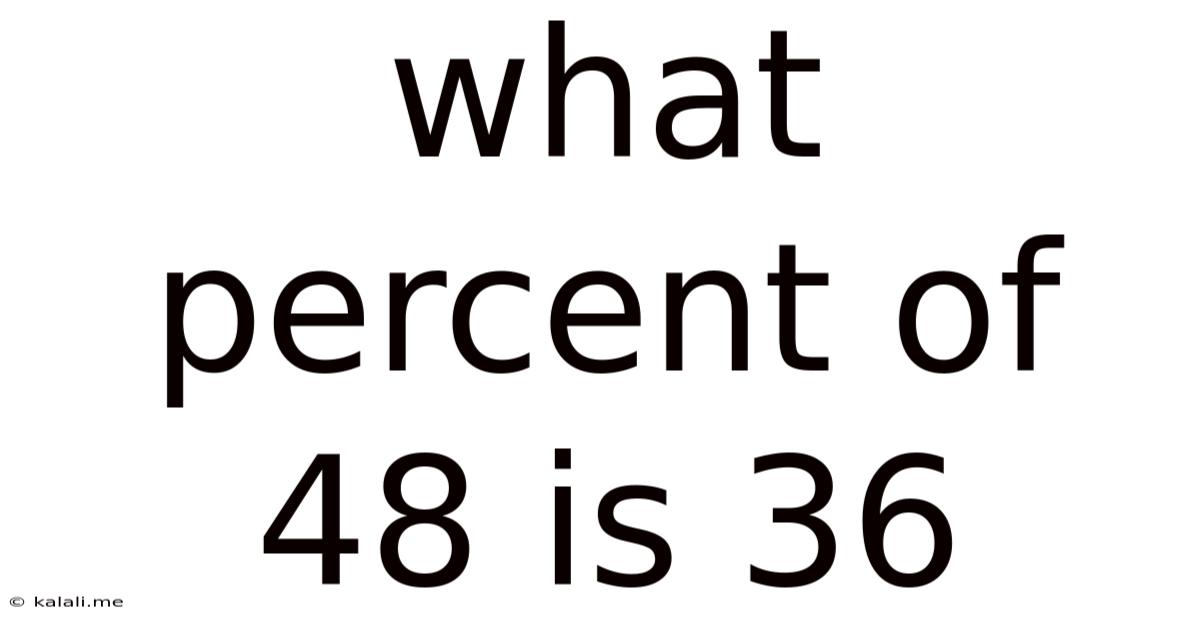
Table of Contents
What Percent of 48 is 36? A Deep Dive into Percentage Calculations
This seemingly simple question, "What percent of 48 is 36?", opens the door to a deeper understanding of percentages, a fundamental concept in mathematics with widespread applications in everyday life, from calculating discounts and taxes to understanding statistics and financial data. This article will not only answer the question directly but also explore the various methods for solving percentage problems, providing a comprehensive guide for anyone looking to master this essential skill. We will delve into the core concepts, different approaches, and practical examples to ensure you gain a solid grasp of percentage calculations.
Understanding Percentages: The Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Understanding this basic definition is key to solving any percentage problem.
Method 1: The Direct Formula Approach
The most straightforward method for solving "What percent of 48 is 36?" involves using a simple formula:
(Part / Whole) x 100 = Percentage
In this case:
- Part: 36 (the number representing the portion of the whole)
- Whole: 48 (the total number)
Substituting these values into the formula:
(36 / 48) x 100 = 75%
Therefore, 36 is 75% of 48.
Method 2: Setting up a Proportion
Another effective approach is setting up a proportion. A proportion is a statement that equates two ratios. We can represent the problem as:
36/48 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
36 x 100 = 48 x
3600 = 48x
x = 3600 / 48
x = 75
Therefore, again, we find that 36 is 75% of 48. This method is particularly useful for visualizing the relationship between the parts and the whole.
Method 3: Using Decimal Equivalents
We can also solve this by converting the fraction 36/48 to a decimal and then multiplying by 100 to express it as a percentage.
36 divided by 48 equals 0.75.
Multiplying 0.75 by 100 gives us 75%.
This approach highlights the connection between fractions, decimals, and percentages, reinforcing the understanding of their inter-relationship. It's a quick and efficient method, especially when dealing with simpler fractions.
Expanding the Understanding: Variations on the Theme
Now that we've solved the core problem, let's explore some related percentage calculations that build upon this foundation:
1. Finding a Percentage of a Number:
Let's say we want to find 20% of 150. We can use the formula:
(Percentage/100) x Number = Result
(20/100) x 150 = 30
Therefore, 20% of 150 is 30.
2. Finding the Whole Given a Percentage and a Part:
If we know that 30 is 15% of a number, we can find the whole number. Let's represent the unknown whole number as 'x'. We can set up the equation:
(15/100) x = 30
Solving for x:
x = 30 x (100/15) = 200
Therefore, 30 is 15% of 200. This type of calculation is common in scenarios involving discounts, where the sale price and the discount percentage are known.
3. Percentage Increase and Decrease:
Percentage changes are frequently encountered in various contexts, like tracking price fluctuations or population growth. To calculate a percentage increase, we use the formula:
[(New Value - Old Value) / Old Value] x 100 = Percentage Increase
Similarly, for a percentage decrease:
[(Old Value - New Value) / Old Value] x 100 = Percentage Decrease
For example, if a price increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] x 100 = 20%
Practical Applications of Percentage Calculations:
The applications of percentage calculations are vast and span across numerous fields:
- Finance: Calculating interest rates, loan repayments, profit margins, investment returns, and tax deductions.
- Retail: Determining discounts, sales prices, and markups.
- Statistics: Analyzing data sets, interpreting survey results, and understanding probability.
- Science: Expressing experimental results, representing ratios, and calculating concentrations.
- Everyday Life: Calculating tips, splitting bills, and understanding nutritional information on food labels.
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The more you practice, the more comfortable you'll become with solving percentage problems.
- Understand the Concepts: Don't just memorize formulas; understand the underlying principles.
- Use Multiple Methods: Try different approaches to see which one works best for you.
- Check Your Work: Always double-check your calculations to avoid errors.
- Use Calculators Wisely: While calculators can be helpful, it's important to understand the underlying calculations to ensure accuracy and avoid over-reliance on technology.
Conclusion: Beyond the Basics
The simple question "What percent of 48 is 36?" has led us on a journey through the fascinating world of percentages. By exploring various methods, understanding their applications, and developing problem-solving skills, you've gained a strong foundation in percentage calculations. This knowledge is not merely academic; it's a practical tool that empowers you to navigate various aspects of daily life and professional endeavors with confidence and accuracy. Remember that continuous practice and a firm grasp of the fundamental concepts are the keys to mastering this essential mathematical skill. So, keep practicing, and you'll soon find yourself effortlessly solving percentage problems in any context they arise.
Latest Posts
Latest Posts
-
18 5 As A Mixed Number
Apr 19, 2025
-
What Is The Prefix Of In
Apr 19, 2025
-
The Ability Of A Substance To Catch Fire Or Burn
Apr 19, 2025
-
35 8 As A Mixed Number
Apr 19, 2025
-
What Is The Domain Of The Function Graphed Below
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 48 Is 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.