What Percent Of 500 Is 25
Kalali
Apr 14, 2025 · 5 min read
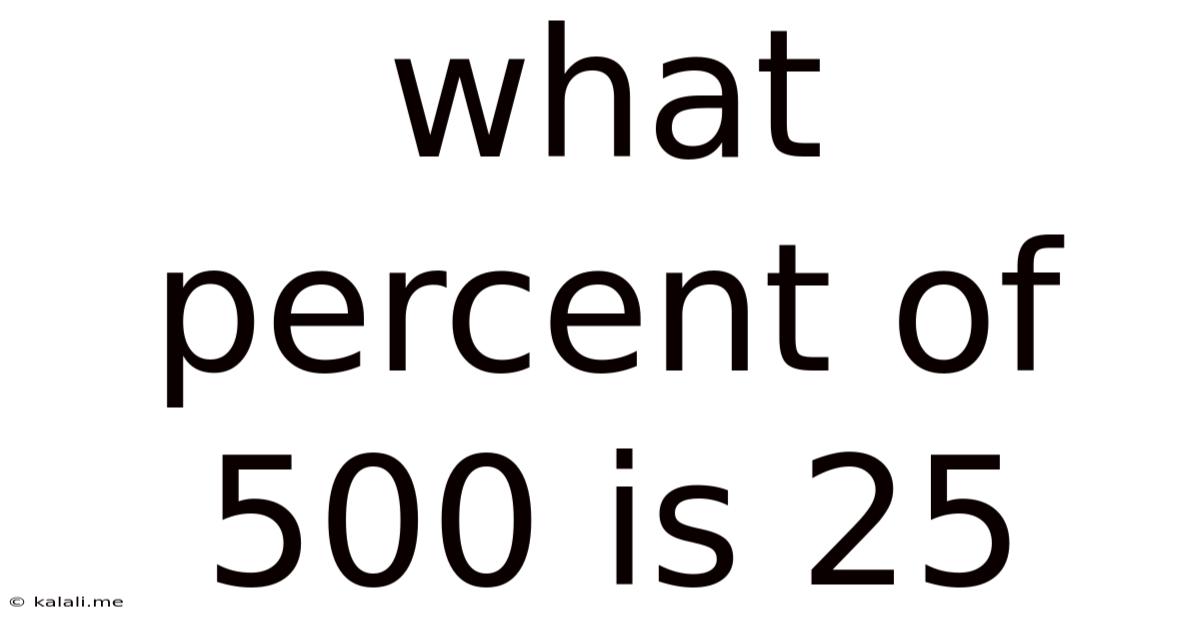
Table of Contents
What Percent of 500 is 25? A Deep Dive into Percentage Calculations and Their Applications
This seemingly simple question, "What percent of 500 is 25?", opens the door to a broader understanding of percentage calculations, their real-world applications, and how to approach similar problems with confidence. This article will not only answer the question directly but will also explore the underlying mathematical principles, provide various methods for solving percentage problems, and illustrate their relevance in diverse fields.
Meta Description: Discover how to calculate percentages easily! This comprehensive guide explains how to find what percent of 500 is 25, explores different calculation methods, and demonstrates real-world applications of percentages in various fields. Learn the essential math skills for tackling percentage problems with confidence.
The answer to "What percent of 500 is 25?" is 5%. But let's unpack how we arrive at this answer and explore the broader context of percentage calculations.
Understanding Percentages: The Fundamentals
A percentage is a fraction or ratio expressed as a number out of 100. The word "percent" comes from the Latin "per centum," meaning "out of a hundred." Percentages are used extensively to represent proportions, changes, and comparisons in various contexts. They provide a standardized way to understand parts relative to a whole.
For example, a score of 80 out of 100 on a test can be expressed as 80%. This immediately conveys the proportion of correct answers relative to the total number of questions. Similarly, a 10% increase in sales indicates a growth of 10 units for every 100 units sold previously.
Methods for Calculating Percentages
There are several ways to calculate percentages, each offering a slightly different approach depending on the context and preferred method. Let's explore a few common methods, using our example of finding what percent of 500 is 25:
Method 1: The Basic Formula
The most fundamental approach involves using the basic percentage formula:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 25
- Whole: 500
Therefore, the calculation is:
(25 / 500) * 100 = 5%
This method is straightforward and works well for most percentage problems.
Method 2: Using Proportions
We can also solve this problem using proportions:
25 / 500 = x / 100
Here, 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
25 * 100 = 500 * x
2500 = 500x
x = 2500 / 500
x = 5
Therefore, x = 5%, confirming our previous result. This method is particularly helpful when dealing with more complex percentage problems involving unknown variables.
Method 3: Decimal Conversion
Another approach is to convert the fraction to a decimal and then multiply by 100:
25 / 500 = 0.05
0.05 * 100 = 5%
This method emphasizes the relationship between decimals and percentages, highlighting that percentages are simply decimals expressed out of 100.
Real-World Applications of Percentage Calculations
Percentages are ubiquitous in everyday life, permeating various sectors and applications. Understanding percentage calculations is crucial for informed decision-making in numerous scenarios:
1. Finance and Business:
- Interest rates: Banks and financial institutions use percentages to calculate interest on loans, savings accounts, and investments. Understanding interest rates is vital for managing personal finances effectively.
- Profit margins: Businesses use percentages to determine profit margins, helping them assess the profitability of their products and services. A higher profit margin suggests greater efficiency and better financial health.
- Sales tax and discounts: Sales tax and discounts are usually expressed as percentages, making it essential to understand percentage calculations for accurate budgeting and shopping.
- Investment returns: Investors track their investment returns as percentages to measure the growth or decline of their portfolios.
- Financial statements: Percentages are crucial in analyzing financial statements like income statements and balance sheets, providing valuable insights into a company's financial performance.
2. Science and Statistics:
- Data analysis: Percentages are frequently used to represent data in graphs, charts, and statistical reports. They help visualize proportions and trends within datasets.
- Experimental results: In scientific experiments, percentages are often used to express the success rate or the proportion of subjects exhibiting a particular outcome.
- Probability and statistics: Probability and statistical analysis extensively rely on percentages to express the likelihood of events occurring.
3. Everyday Life:
- Tips and gratuities: Restaurant tips and service charges are usually expressed as percentages of the total bill.
- Surveys and polls: Survey results and public opinion polls often present data as percentages, making it easy to understand the distribution of opinions.
- Recipe scaling: When adjusting recipes, percentages are helpful in scaling ingredient quantities up or down proportionally.
- Sales and promotions: Understanding percentage discounts helps consumers make informed purchasing decisions.
Advanced Percentage Problems and Techniques
While the problem "What percent of 500 is 25?" is relatively straightforward, more complex percentage problems require a deeper understanding of algebraic manipulation and problem-solving strategies. Here are a few examples of more advanced scenarios:
- Finding the whole when the percentage and part are known: For instance, if 20% of a number is 50, what is the number? This involves rearranging the basic percentage formula.
- Finding the part when the percentage and whole are known: For instance, what is 15% of 800? This involves directly applying the basic formula.
- Calculating percentage change (increase or decrease): This involves comparing two values and determining the percentage difference between them. This is commonly used in analyzing economic data, sales figures, or population growth.
- Compound percentages: This involves calculating percentages on percentages, often used in compound interest calculations or in situations where percentage changes occur repeatedly.
These advanced problems necessitate a stronger grasp of algebraic principles and the ability to manipulate equations to solve for unknown variables. Practice and familiarity with different problem types are key to mastering these skills.
Conclusion: Mastering Percentages for Success
The seemingly simple question, "What percent of 500 is 25?", serves as a gateway to understanding the multifaceted world of percentage calculations. This article explored multiple methods for solving percentage problems, highlighted their widespread applications across various fields, and touched upon more complex scenarios. Mastering percentage calculations is not just a valuable mathematical skill; it's a crucial life skill, empowering individuals to make informed decisions, analyze data effectively, and navigate the complexities of the modern world with confidence. Consistent practice and exposure to diverse problem types are essential for developing a strong grasp of percentage calculations and their practical applications. Remember to always approach percentage problems systematically, break them down into manageable steps, and choose the most suitable method based on the specific details of the problem.
Latest Posts
Latest Posts
-
5 Is What Percent Of 50
Apr 15, 2025
-
What Is 3 And 1 8 As A Decimal
Apr 15, 2025
-
6 Out Of 10 Percentage Grade
Apr 15, 2025
-
What Is 8 Out Of 9 As A Percentage
Apr 15, 2025
-
A Bunch Of Amino Acids Attached Together Is Called A
Apr 15, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 500 Is 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.