What Percent Of 60 Is 42
Kalali
Apr 18, 2025 · 5 min read
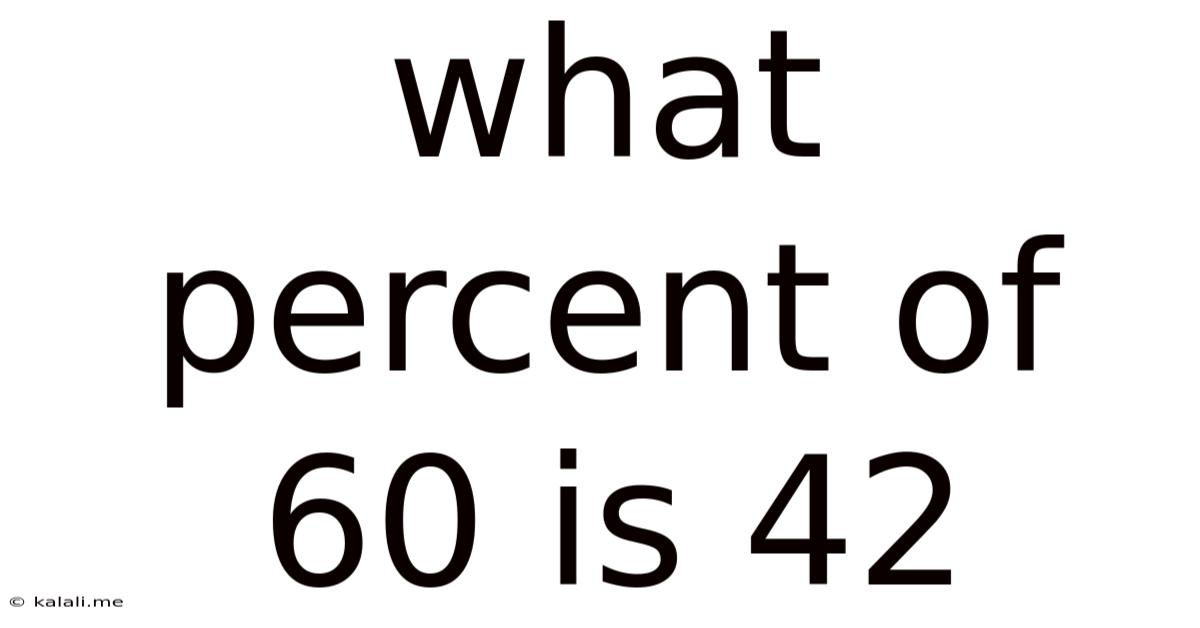
Table of Contents
What Percent of 60 is 42? A Deep Dive into Percentage Calculations
What percent of 60 is 42? This seemingly simple question opens the door to a broader understanding of percentages, their applications, and the various methods used to solve percentage problems. This article will not only answer the question directly but also explore the underlying concepts, providing you with a comprehensive guide to tackling similar problems with confidence. We'll cover different calculation methods, real-world applications, and even touch upon advanced percentage concepts.
Understanding Percentages: The Foundation
Before diving into the solution, let's establish a solid understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "per cent" or "out of one hundred." Understanding this fundamental definition is crucial for grasping percentage calculations. For example, 50% means 50 out of 100, which simplifies to 1/2 or 0.5.
Method 1: Using Proportions to Solve "What Percent of 60 is 42?"
This method utilizes the power of proportions – two equal ratios. We can set up a proportion to solve for the unknown percentage:
- Part / Whole = Percentage / 100
In our problem:
- Part = 42
- Whole = 60
- Percentage = x (what we need to find)
Substituting these values into our proportion equation:
- 42 / 60 = x / 100
To solve for 'x', we cross-multiply:
- 42 * 100 = 60 * x
- 4200 = 60x
Now, divide both sides by 60:
- x = 4200 / 60
- x = 70
Therefore, 42 is 70% of 60.
Method 2: Using Decimal Conversion
This method involves converting the percentage into a decimal and then performing a simple calculation. We can express "x percent of 60 is 42" as an equation:
- (x/100) * 60 = 42
To solve for 'x':
- Divide both sides by 60: (x/100) = 42 / 60 = 0.7
- Multiply both sides by 100: x = 0.7 * 100 = 70
Again, we arrive at the answer: 42 is 70% of 60.
Method 3: The "Is Over Of" Method
This is a simplified approach, especially helpful for quick mental calculations or when dealing with simpler percentage problems. The formula is:
- (Part / Whole) * 100 = Percentage
Plugging in our values:
- (42 / 60) * 100 = 0.7 * 100 = 70%
This method directly translates the wording of the problem into a mathematical equation, making it intuitive and easy to remember.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous everyday situations:
-
Sales and Discounts: Calculating discounts on products, understanding sales tax, and determining the final price after applying discounts and taxes all involve percentage calculations. For example, a 20% discount on a $100 item means a savings of $20 ($100 * 0.20 = $20).
-
Finance and Investments: Calculating interest earned on savings accounts, understanding returns on investments, and analyzing financial statements all rely heavily on percentage calculations. Understanding interest rates, both simple and compound, requires proficiency in percentages.
-
Statistics and Data Analysis: Percentages are frequently used to represent proportions and trends in data. For instance, expressing survey results, analyzing market share, and illustrating demographic trends all involve percentages.
-
Science and Engineering: Percentages are utilized in various scientific fields, from calculating concentrations of solutions in chemistry to expressing efficiency in engineering.
-
Everyday Life: Calculating tips at restaurants, determining the percentage of completion of a task, or understanding nutritional information on food labels all involve percentage calculations.
Advanced Percentage Concepts and Problem Solving
While the basic percentage calculation is relatively straightforward, several advanced concepts can further enhance your understanding and problem-solving abilities:
-
Percentage Increase and Decrease: These calculations determine the percentage change between two values. For example, if a price increases from $50 to $60, the percentage increase is 20% [(($60-$50)/$50) * 100]. Conversely, a decrease from $60 to $50 represents a 16.7% decrease [(($60-$50)/$60) * 100].
-
Compound Interest: This concept involves calculating interest not only on the principal amount but also on the accumulated interest from previous periods. Compound interest calculations are more complex than simple interest calculations and require a deeper understanding of exponential growth.
-
Percentage Points: This term refers to the arithmetic difference between two percentages. For example, an increase from 10% to 15% is a 5 percentage point increase, not a 50% increase. This distinction is crucial in interpreting data and avoiding misinterpretations.
-
Solving for Other Variables: In percentage problems, you might need to solve for the "whole" or the "part" instead of the percentage. Understanding how to rearrange the equations to solve for these different variables is essential.
Tips for Mastering Percentage Calculations
-
Practice Regularly: Consistent practice is key to mastering any mathematical concept. Solve a variety of problems, gradually increasing their complexity.
-
Understand the Concepts: Don't just memorize formulas; understand the underlying principles of percentages. This understanding will help you adapt to different problem types.
-
Use Different Methods: Try different approaches to solve the same problem. This helps you develop a deeper understanding and identify the method best suited to your style.
-
Check Your Answers: Always verify your calculations to ensure accuracy. Using a calculator can help with more complex problems, but it's also important to develop mental estimation skills.
-
Seek Help When Needed: Don't hesitate to seek clarification if you encounter difficulties. Online resources, textbooks, and tutors can provide valuable support.
Conclusion: Beyond the Simple Answer
The answer to "What percent of 60 is 42?" is definitively 70%. However, the true value of this article lies not just in the solution but in the comprehensive exploration of percentage calculations. By understanding the underlying concepts, mastering different calculation methods, and recognizing real-world applications, you gain a valuable skill applicable across numerous disciplines. This understanding empowers you to confidently tackle percentage problems in your personal and professional life, making you a more effective problem-solver and decision-maker. Remember to practice regularly and explore the advanced concepts to fully harness the power of percentage calculations.
Latest Posts
Latest Posts
-
What Percent Of 60 Is 10
Apr 19, 2025
-
How Many Oz Of Butter Is 1 Cup
Apr 19, 2025
-
78 Inches In Feet And Inches
Apr 19, 2025
-
Cuanto Es 13 Grados Fahrenheit En Centigrados
Apr 19, 2025
-
How Much Is 39 Degrees Celsius In Fahrenheit
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 60 Is 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.