What Percent Of 60 Is 50
Kalali
Apr 16, 2025 · 5 min read
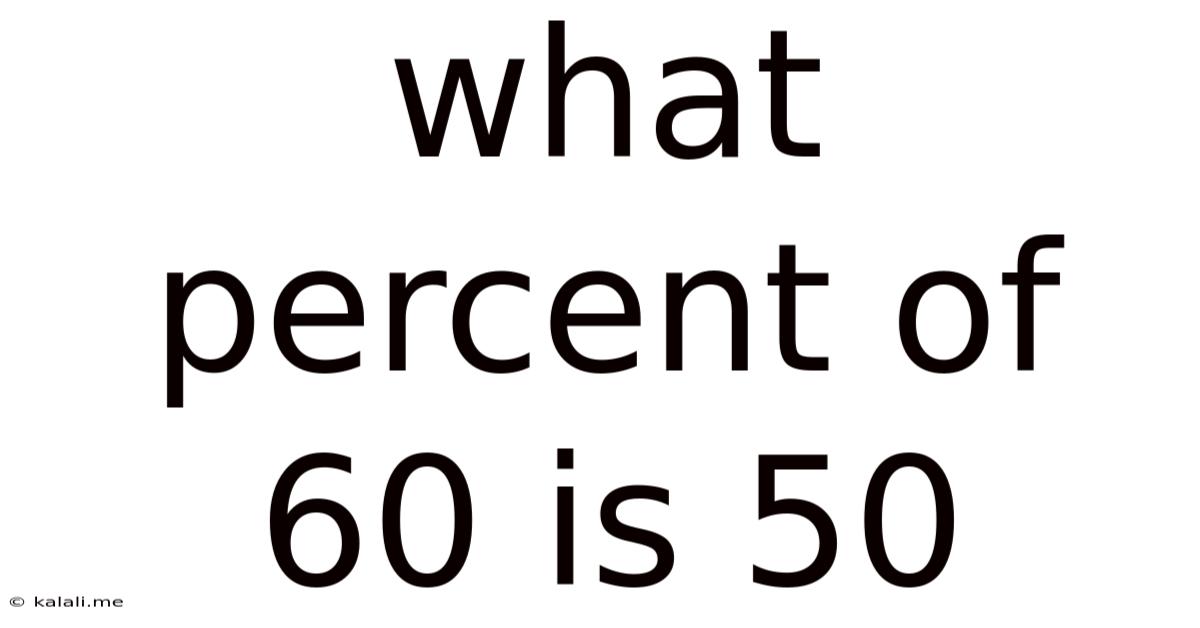
Table of Contents
What Percent of 60 is 50? A Comprehensive Guide to Percentage Calculations
What percent of 60 is 50? This seemingly simple question delves into the fundamental concepts of percentages, a crucial mathematical skill applicable across numerous fields, from finance and statistics to everyday life. This article will not only answer this specific question but also provide a comprehensive understanding of percentage calculations, offering various methods and practical applications. Understanding percentages is key to interpreting data, making informed decisions, and navigating the numerical world around us.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of 100" (per centum in Latin). Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. Percentages are widely used to represent proportions, ratios, and changes in values.
Method 1: Using Proportions
The most straightforward approach to solving "What percent of 60 is 50?" involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can express the problem as:
x/100 = 50/60
Where 'x' represents the percentage we are trying to find. To solve for x, we cross-multiply:
60x = 50 * 100
60x = 5000
x = 5000 / 60
x ≈ 83.33
Therefore, 50 is approximately 83.33% of 60.
Method 2: Using the Percentage Formula
The percentage formula provides a more direct approach:
Percentage = (Part / Whole) * 100
In our problem:
- Part = 50
- Whole = 60
Plugging these values into the formula:
Percentage = (50 / 60) * 100
Percentage ≈ 83.33%
This confirms our previous result. This method is efficient and easily adaptable to various percentage problems.
Method 3: Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
First, express the relationship as a fraction: 50/60
Simplify the fraction (if possible): 5/6
Convert the fraction to a decimal by dividing the numerator by the denominator: 5 ÷ 6 ≈ 0.8333
Multiply the decimal by 100 to obtain the percentage: 0.8333 * 100 ≈ 83.33%
Practical Applications of Percentage Calculations
Understanding percentage calculations has wide-ranging applications in various aspects of life:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For example, understanding the annual percentage rate (APR) on a loan is crucial for financial planning. Similarly, calculating sales tax or discounts at the store involves applying percentages to the original price.
-
Statistics: Percentages are fundamental to interpreting statistical data. Representing data as percentages helps in comparing different groups, visualizing trends, and drawing meaningful conclusions. For example, understanding unemployment rates, population growth, or survey results often requires percentage analysis.
-
Science: Percentages are commonly used in scientific studies to express concentrations, yields, and error rates. For instance, the concentration of a solution is often expressed as a percentage.
-
Everyday Life: Calculating tips at restaurants, determining the sale price of an item, understanding nutritional information on food labels, and comparing prices of different products all involve percentage calculations.
Advanced Percentage Problems and Scenarios
While the initial problem was relatively straightforward, let's explore more complex scenarios:
- Finding the Whole: If we know that 20% of a number is 15, how can we find the original number? This requires reversing the percentage formula:
Whole = (Part / Percentage) * 100
Whole = (15 / 20) * 100 = 75
- Percentage Increase/Decrease: Calculating percentage change is crucial in tracking growth or decline. The formula for percentage increase is:
Percentage Increase = [(New Value - Old Value) / Old Value] * 100
Similarly, for percentage decrease:
Percentage Decrease = [(Old Value - New Value) / Old Value] * 100
These formulas are essential for analyzing trends in sales, profits, stock prices, and population demographics.
-
Compound Interest: Compound interest involves earning interest on both the principal amount and accumulated interest. This concept is critical in long-term investments and loan calculations, requiring a more complex formula involving exponential growth.
-
Percentage Points vs. Percentages: It's essential to differentiate between percentage points and percentages. A change from 20% to 30% is a 10 percentage point increase, but a 50% increase (10/20 * 100). This distinction is crucial for accurate interpretation of data.
Tips for Mastering Percentage Calculations
-
Practice Regularly: The key to mastering percentages is consistent practice. Solve various problems, starting with simple ones and gradually progressing to more complex scenarios.
-
Utilize Online Resources: Numerous online resources, including calculators, tutorials, and practice exercises, can aid in understanding and mastering percentage calculations.
-
Understand the Underlying Concepts: Don't just memorize formulas; understand the logic behind them. This will help you adapt your approach to different problems and apply percentage calculations effectively in various contexts.
-
Check Your Work: Always verify your calculations to ensure accuracy. Use different methods to cross-check your answers.
-
Break Down Complex Problems: When faced with complex problems, break them down into smaller, manageable steps. This will simplify the process and make it easier to solve the problem systematically.
Conclusion
In conclusion, 50 is approximately 83.33% of 60. This seemingly simple question opens the door to a vast world of percentage calculations. Mastering these calculations is crucial for navigating the numerical aspects of finance, statistics, science, and everyday life. By understanding the different methods, formulas, and applications of percentages, you can enhance your analytical skills and make informed decisions in various situations. Remember to practice regularly, utilize available resources, and focus on understanding the underlying concepts to truly master this essential mathematical skill.
Latest Posts
Latest Posts
-
500 Inches Is How Many Feet
Apr 19, 2025
-
18 5 As A Mixed Number
Apr 19, 2025
-
What Is The Prefix Of In
Apr 19, 2025
-
The Ability Of A Substance To Catch Fire Or Burn
Apr 19, 2025
-
35 8 As A Mixed Number
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 60 Is 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.