What Percent Of 75 Is 10
Kalali
Apr 24, 2025 · 5 min read
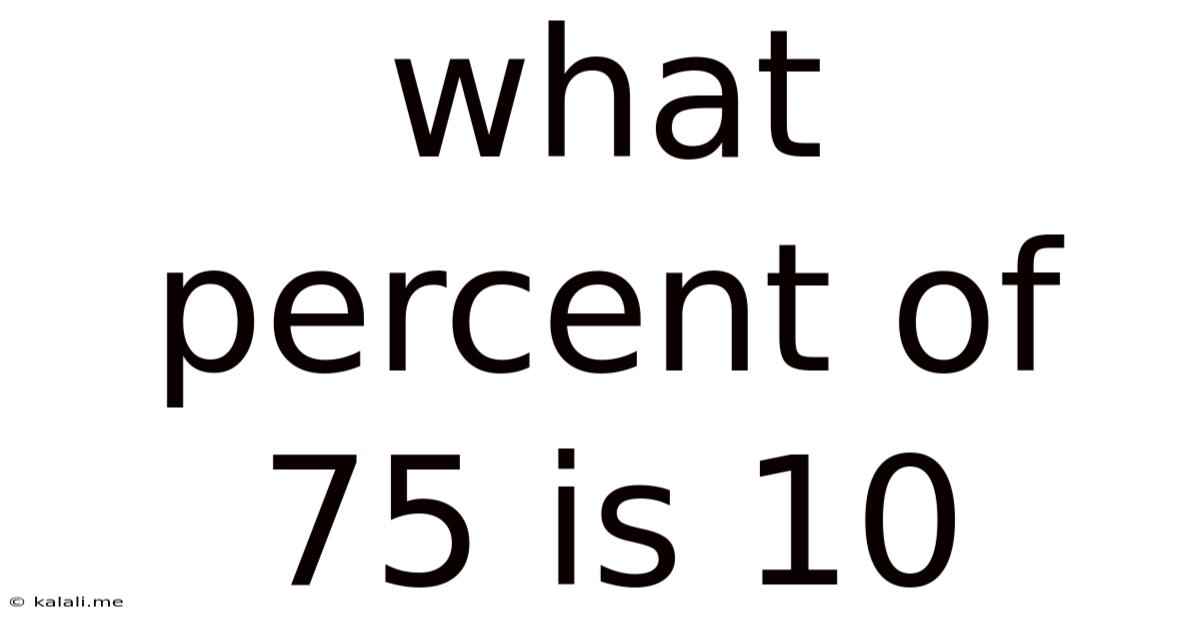
Table of Contents
What Percent of 75 is 10? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "What percent of 75 is 10?", opens the door to a broader understanding of percentage calculations – a fundamental skill in various fields, from everyday budgeting to advanced statistical analysis. This article will not only answer the question directly but also delve into the underlying principles, providing you with the tools to solve similar problems and even tackle more complex percentage scenarios. We'll explore different methods, illustrate with examples, and offer practical applications.
Understanding Percentages: The Foundation
A percentage is a fraction expressed as a number out of 100. It represents a portion or proportion of a whole. The symbol "%" denotes percentage. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. Understanding this basic concept is crucial for tackling percentage calculations effectively.
Method 1: Using the Proportion Method
This is a classic and intuitive approach for solving percentage problems. We set up a proportion, equating two ratios:
- Ratio 1: The given part (10) to the whole (75)
- Ratio 2: The unknown percentage (x) to 100
This can be written as:
10/75 = x/100
To solve for x (the percentage), we cross-multiply:
10 * 100 = 75 * x
1000 = 75x
x = 1000 / 75
x ≈ 13.33
Therefore, 10 is approximately 13.33% of 75.
Method 2: Using the Decimal Method
This method involves converting the percentage to a decimal and then performing the calculation.
First, we represent the problem as an equation:
x * 75 = 10
To isolate x, we divide both sides by 75:
x = 10 / 75
x ≈ 0.1333
Now, to convert this decimal back into a percentage, we multiply by 100:
x ≈ 0.1333 * 100
x ≈ 13.33%
This confirms our result from the proportion method.
Method 3: Using a Calculator
Modern calculators often have a percentage function. Simply input the calculation as (10 / 75) * 100 and press the equals button. This will directly give you the answer: 13.33%. This method is the fastest and most convenient for straightforward calculations.
Practical Applications of Percentage Calculations
Understanding percentage calculations has countless practical uses. Here are a few examples:
-
Discounts: Determining the final price of an item after a discount is applied. For example, a 20% discount on a $50 item means a reduction of $10 (20% of $50).
-
Taxes: Calculating sales tax or income tax. A 6% sales tax on a $100 purchase adds $6 to the total cost.
-
Tips: Determining the appropriate tip amount in a restaurant. A 15% tip on a $75 bill is approximately $11.25.
-
Financial Analysis: Evaluating investment returns, profit margins, and other key financial metrics. A 10% increase in investment value represents significant growth.
-
Statistics: Interpreting statistical data and analyzing trends. Percentages are essential for expressing proportions and changes in data.
-
Scientific Research: Expressing experimental results, such as the percentage of participants responding positively to a treatment.
-
Everyday Life: Calculating proportions of ingredients in recipes, understanding sale prices, and even figuring out savings on energy bills.
Solving More Complex Percentage Problems
While the "What percent of 75 is 10?" problem is relatively straightforward, the methods discussed can be adapted to solve more complex percentage problems. Let's explore a few variations:
1. Finding the Percentage Increase or Decrease:
Suppose a quantity increases from 50 to 60. To find the percentage increase:
- Difference: 60 - 50 = 10
- Percentage increase: (10 / 50) * 100 = 20%
Similarly, if a quantity decreases from 60 to 50, the percentage decrease would be:
- Difference: 60 - 50 = 10
- Percentage decrease: (10 / 60) * 100 ≈ 16.67%
2. Finding a Specific Percentage of a Number:
What is 25% of 200?
- Calculation: (25/100) * 200 = 50
3. Finding the Original Value After a Percentage Change:
An item costs $75 after a 10% increase. What was the original price?
Let 'x' be the original price. Then:
x + 0.10x = 75
1.10x = 75
x = 75 / 1.10
x ≈ 68.18
The original price was approximately $68.18.
4. Finding the Whole when a Percentage is Known:
15% of a number is 30. What is the number?
Let 'x' be the number. Then:
0.15x = 30
x = 30 / 0.15
x = 200
The number is 200.
Advanced Percentage Concepts and Techniques
While the fundamental methods covered above suffice for many situations, understanding more advanced concepts can be beneficial for tackling complex problems:
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. This is a common concept in finance and investments.
-
Weighted Averages: Calculating averages where different data points have varying importance or weights. This is often used in statistics and finance.
-
Percentage Points vs. Percentage Change: It's crucial to differentiate between these two. A change from 20% to 30% is a 10 percentage point increase, but a 50% percentage increase (10/20 * 100%).
-
Using Spreadsheets and Software: Tools like Microsoft Excel or Google Sheets provide built-in functions for complex percentage calculations, simplifying analysis and automation.
Conclusion:
The seemingly simple question, "What percent of 75 is 10?", serves as a springboard to understanding the power and versatility of percentage calculations. Mastering these techniques empowers you to solve a vast array of problems in various contexts, from everyday finances to more advanced mathematical and statistical applications. By understanding the fundamental methods, and practicing with different problem types, you can build confidence and competence in handling percentages effectively. Remember that the key to success lies in understanding the underlying principles and adapting your approach to the specific problem at hand.
Latest Posts
Latest Posts
-
170 Cm Is How Many Inches
Apr 24, 2025
-
Whats The Square Root Of 4
Apr 24, 2025
-
Which Protist Exhibits Both Animal Like And Plant Like Characteristics
Apr 24, 2025
-
3 4 As A Whole Number
Apr 24, 2025
-
How Many Cups Of Water In 16 9 Fl Oz
Apr 24, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 75 Is 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.