What Percentage Is 26 Out Of 30
Kalali
Apr 22, 2025 · 5 min read
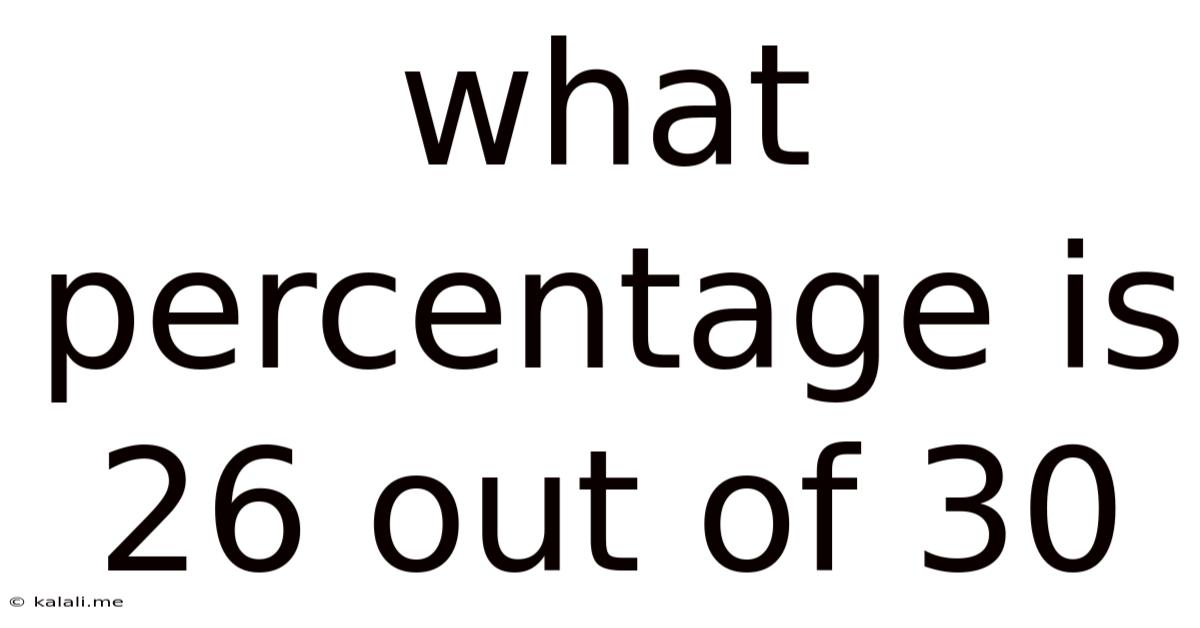
Table of Contents
What Percentage is 26 out of 30? A Comprehensive Guide to Percentage Calculations
Meta Description: Learn how to calculate percentages, specifically determining what percentage 26 out of 30 represents. This guide covers the basic formula, step-by-step instructions, real-world applications, and advanced percentage calculations.
Understanding percentages is a fundamental skill applicable across numerous fields, from academic studies and financial planning to everyday life situations. This comprehensive guide will walk you through calculating the percentage that 26 represents out of 30, explaining the process clearly and providing additional context to enhance your understanding of percentage calculations. We'll cover the basic formula, illustrate the solution with a step-by-step approach, explore real-world applications, and delve into more advanced percentage problems.
The Basic Percentage Formula
The fundamental formula for calculating percentages is:
(Part / Whole) x 100% = Percentage
In this formula:
- Part: Represents the specific value you're interested in expressing as a percentage. In our case, the part is 26.
- Whole: Represents the total value against which the part is compared. In our case, the whole is 30.
- Percentage: The final result, indicating the proportional representation of the part relative to the whole.
Calculating the Percentage: 26 out of 30
Let's apply the formula to determine what percentage 26 out of 30 represents:
-
Identify the Part and the Whole:
- Part = 26
- Whole = 30
-
Substitute into the Formula:
- (26 / 30) x 100% = Percentage
-
Calculate the Fraction:
- 26 / 30 = 0.866666...
-
Multiply by 100%:
- 0.866666... x 100% ≈ 86.67%
Therefore, 26 out of 30 is approximately 86.67%.
Understanding the Result: Meaning and Interpretation
The result, 86.67%, signifies that 26 represents approximately 86.67% of the total value 30. This percentage provides a concise way to express the proportional relationship between the two numbers. It’s crucial to understand that this percentage is a relative value; it depends entirely on the context and the relationship between the part and the whole.
Real-World Applications of Percentage Calculations
Percentage calculations are essential tools with broad applicability in various real-world scenarios. Here are a few examples:
-
Academic Performance: Calculating grades based on the number of correctly answered questions on a test. For instance, if a student answered 26 questions correctly out of 30, their score would be 86.67%.
-
Financial Matters: Determining discounts, interest rates, tax rates, profit margins, and investment returns frequently involve percentage calculations. A 10% discount on a $100 item would be $10, calculated as (10/100) * $100.
-
Statistics and Data Analysis: Percentages are extensively used to represent data proportions in charts, graphs, and reports, making complex data more accessible and understandable. For example, presenting the percentage of respondents who favored a particular candidate in a survey.
-
Everyday Life: Calculating tips in restaurants, determining sales tax, or understanding the nutritional information on food labels all involve percentage calculations.
Advanced Percentage Calculations and Related Concepts
While the basic percentage formula is straightforward, several related concepts can enhance your understanding and ability to handle more complex scenarios:
-
Calculating the Part: If you know the percentage and the whole, you can calculate the part using the following formula:
(Percentage / 100%) x Whole = PartFor example, what is 25% of 80? (25/100) * 80 = 20
-
Calculating the Whole: If you know the percentage and the part, you can find the whole using this formula:
(Part / Percentage) x 100% = WholeFor example, if 20 is 25%, what is the whole? (20/25) * 100 = 80
-
Percentage Increase and Decrease: These concepts are crucial for understanding changes in values over time. To calculate a percentage increase:
[(New Value - Old Value) / Old Value] x 100% = Percentage IncreaseTo calculate a percentage decrease:
[(Old Value - New Value) / Old Value] x 100% = Percentage Decrease -
Percentage Points: It's important to differentiate between percentage points and percentage changes. A change from 20% to 30% is a 10 percentage point increase, but a 50% increase in the percentage itself.
-
Compounding Percentages: In situations where percentages are applied repeatedly (like compound interest), the calculations become more complex. The effect of compounding can significantly alter the final outcome.
Practical Examples of Advanced Percentage Calculations
Let's illustrate some practical examples to further solidify your understanding:
Example 1: Percentage Increase
A product originally cost $50. The price increased to $65. What is the percentage increase?
[(65 - 50) / 50] x 100% = 30% increase
Example 2: Percentage Decrease
A store initially had 100 items in stock. After a sale, only 70 items remained. What's the percentage decrease?
[(100 - 70) / 100] x 100% = 30% decrease
Example 3: Calculating the Whole
If 15 represents 30% of a total, what is the total value?
(15 / 30) x 100 = 50
Example 4: Compound Interest (simplified)
Imagine investing $1000 at a 5% annual interest rate compounded annually. After two years, the value will be:
Year 1: $1000 + ($1000 x 0.05) = $1050 Year 2: $1050 + ($1050 x 0.05) = $1102.50
Note: This is a simplified example. Real-world compound interest calculations often involve more complex formulas depending on the compounding frequency.
Conclusion: Mastering Percentage Calculations
Understanding and applying percentage calculations is a valuable skill with numerous applications across various fields. From everyday tasks to complex financial analyses, mastering percentage calculations empowers you to make informed decisions and interpret data effectively. This guide has provided a thorough exploration of basic and advanced percentage concepts, equipping you with the tools needed to confidently approach and solve percentage-related problems in diverse situations. Remember to always carefully identify the part and the whole in each problem to ensure accurate results. Practice is key; the more you work with percentages, the more comfortable and proficient you'll become.
Latest Posts
Latest Posts
-
Elements In Group 17 Are Called
Apr 22, 2025
-
How Long Is 200 Cm In Inches
Apr 22, 2025
-
What Percent Is 12 Of 16
Apr 22, 2025
-
Convert 16 Degrees C To Fahrenheit
Apr 22, 2025
-
32 Oz Is Equal To How Many Cups
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 26 Out Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.