What Percentage Is 28 Out Of 40
Kalali
Apr 08, 2025 · 5 min read
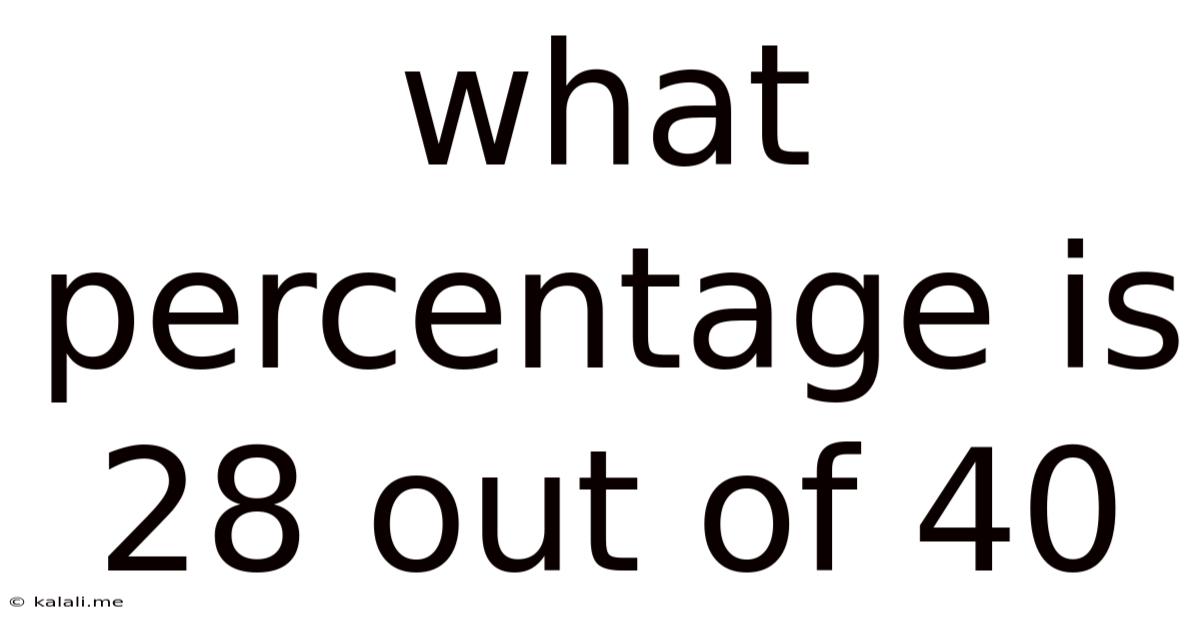
Table of Contents
What Percentage is 28 out of 40? A Comprehensive Guide to Percentage Calculations
Determining what percentage 28 represents out of 40 might seem like a simple calculation, but understanding the underlying principles is crucial for various applications, from academic assignments to real-world scenarios involving budgeting, performance analysis, and more. This comprehensive guide will not only answer the question directly but will also equip you with the knowledge and tools to tackle similar percentage problems with confidence. We'll explore different methods, discuss the concept of percentages thoroughly, and delve into practical examples.
Meta Description: Learn how to calculate percentages effortlessly! This detailed guide explains how to find what percentage 28 is out of 40, covering multiple methods and providing practical applications for various scenarios. Master percentage calculations with clear examples and step-by-step instructions.
Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself originates from the Latin "per centum," meaning "out of one hundred." Therefore, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. This fundamental understanding forms the basis for all percentage calculations.
Method 1: The Basic Formula
The most straightforward method to calculate the percentage involves a simple formula:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 28
- Whole: 40
Plugging these values into the formula:
(28 / 40) x 100% = 70%
Therefore, 28 is 70% of 40.
Method 2: Using Decimal Equivalents
Another approach involves converting the fraction to a decimal first and then multiplying by 100%.
- Convert the fraction to a decimal: 28 / 40 = 0.7
- Multiply by 100%: 0.7 x 100% = 70%
This method is particularly useful when working with calculators or when dealing with more complex fractions.
Method 3: Simplifying the Fraction
Before applying the formula, simplifying the fraction can make the calculation easier. In this case, both 28 and 40 are divisible by 4:
28 / 40 simplifies to 7 / 10
Now, applying the formula:
(7 / 10) x 100% = 70%
This method showcases the importance of understanding fraction simplification, a vital skill in mathematics.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in various real-world applications:
- Academic Performance: Calculating grades, understanding test scores, and assessing overall academic progress. For example, if a student scored 28 out of 40 on a test, their percentage score is 70%.
- Financial Management: Budgeting, calculating discounts, understanding interest rates, and analyzing investment returns. Knowing what percentage of your income is allocated to different expenses is crucial for sound financial planning.
- Business and Economics: Analyzing sales figures, calculating profit margins, assessing market share, and tracking economic indicators. Understanding percentage changes in sales or profits can greatly inform business decisions.
- Data Analysis and Statistics: Presenting data in a clear and concise manner, interpreting statistical results, and making informed decisions based on quantitative information. Percentages are frequently used in charts and graphs to illustrate data effectively.
- Everyday Life: Calculating tips, determining discounts at stores, understanding sales tax, and even figuring out the percentage of ingredients in a recipe. Percentages are woven into the fabric of our daily lives.
Advanced Percentage Problems: Finding the Whole or the Part
While the problem at hand focused on finding the percentage, percentage calculations can also involve finding the whole or the part when the percentage and one of the other values are known. Let's explore these scenarios:
Scenario 1: Finding the Whole
Problem: 70% of a number is 28. What is the number?
Solution: We can set up an equation:
0.70 * x = 28
Solving for x:
x = 28 / 0.70 = 40
Therefore, the whole number is 40.
Scenario 2: Finding the Part
Problem: What is 30% of 40?
Solution:
0.30 * 40 = 12
Therefore, 30% of 40 is 12.
Percentage Increase and Decrease
Percentage calculations also extend to determining the percentage increase or decrease between two numbers. This is frequently used to track changes over time, such as population growth, economic fluctuations, or sales trends.
Scenario 3: Percentage Increase
Problem: A product's price increased from 20 to 28. What is the percentage increase?
Solution:
- Find the difference: 28 - 20 = 8
- Divide the difference by the original value: 8 / 20 = 0.4
- Multiply by 100%: 0.4 x 100% = 40%
The price increased by 40%.
Scenario 4: Percentage Decrease
Problem: The number of students in a class decreased from 40 to 32. What is the percentage decrease?
Solution:
- Find the difference: 40 - 32 = 8
- Divide the difference by the original value: 8 / 40 = 0.2
- Multiply by 100%: 0.2 x 100% = 20%
The number of students decreased by 20%.
Using Calculators and Spreadsheets
For more complex calculations involving percentages, utilizing calculators or spreadsheets like Microsoft Excel or Google Sheets can significantly streamline the process. These tools offer built-in functions for percentage calculations, making it easy to perform various operations efficiently. In Excel, for instance, the formula =(28/40)*100 would directly provide the answer.
Conclusion
Determining that 28 out of 40 is 70% is a fundamental percentage calculation. However, understanding the underlying principles, methods, and various applications allows for broader application in numerous scenarios. From simple calculations to more advanced problems involving finding the whole, the part, or percentage increase/decrease, mastering percentage calculations equips you with a valuable skill applicable across various aspects of life and work. Remember to practice regularly, and use the methods and examples discussed here to build your confidence and proficiency in percentage calculations. With consistent practice, these calculations will become second nature.
Latest Posts
Latest Posts
-
How Much Is 40 In Cm
Apr 17, 2025
-
What Is 25 Off Of 30
Apr 17, 2025
-
71 In Is How Many Feet
Apr 17, 2025
-
An Inclined Plane Wrapped Around A Cylinder
Apr 17, 2025
-
What Is A Quarter Of 12
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 28 Out Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.