What Percentage Of 20 Is 16
Kalali
Apr 10, 2025 · 5 min read
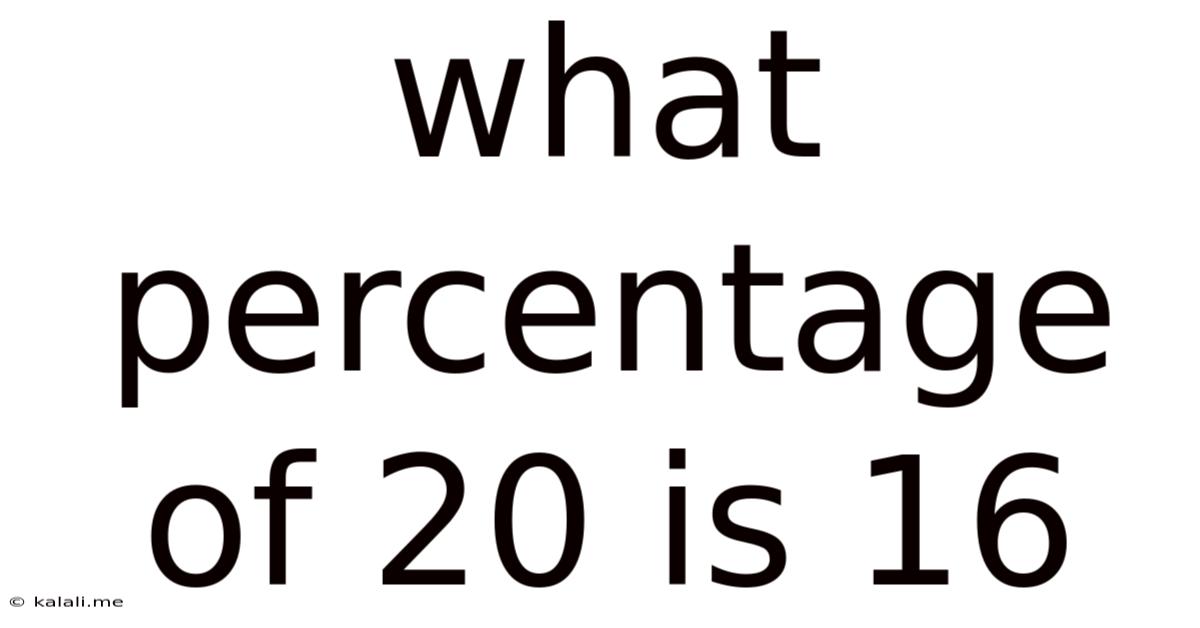
Table of Contents
What Percentage of 20 is 16? A Comprehensive Guide to Percentage Calculations
This article will delve into the seemingly simple question: "What percentage of 20 is 16?" While the answer might seem immediately obvious to some, understanding the underlying methodology is crucial for tackling more complex percentage problems. We'll not only solve this specific problem but also explore the broader concepts of percentages, their applications, and different methods for calculating them. This guide is designed for everyone, from those brushing up on their math skills to those looking to improve their data analysis capabilities.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to determine what percentage 16 is of 20. This guide covers various methods and real-world applications of percentage calculations.
Understanding Percentages
Before diving into the calculation, let's establish a firm understanding of what percentages represent. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "per cent" or "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to ½ or 0.5. Percentages are used extensively in various fields, including finance, statistics, science, and everyday life. They provide a standardized way to compare proportions and express changes.
Method 1: The Proportion Method
This is perhaps the most straightforward method for solving "What percentage of 20 is 16?". We set up a proportion:
- Part/Whole = Percentage/100
In our case:
- Part = 16
- Whole = 20
- Percentage = x (what we need to find)
Substituting these values into the proportion:
- 16/20 = x/100
To solve for x, we cross-multiply:
- 16 * 100 = 20 * x
- 1600 = 20x
Now, divide both sides by 20:
- x = 1600 / 20
- x = 80
Therefore, 16 is 80% of 20.
Method 2: The Decimal Method
This method involves converting the fraction to a decimal and then multiplying by 100 to express it as a percentage.
First, we express the relationship as a fraction:
- 16/20
Next, we simplify the fraction (if possible):
- 16/20 = 4/5
Now, we convert the fraction to a decimal by dividing the numerator by the denominator:
- 4 ÷ 5 = 0.8
Finally, we multiply the decimal by 100 to express it as a percentage:
- 0.8 * 100 = 80%
Again, we arrive at the answer: 16 is 80% of 20.
Method 3: Using a Calculator
Most calculators have a percentage function. The process is usually straightforward:
- Divide 16 by 20: 16 ÷ 20 = 0.8
- Multiply the result by 100: 0.8 * 100 = 80
- The answer is 80%.
This method is the quickest and most efficient, especially for more complex percentage calculations.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is invaluable in numerous real-world scenarios. Here are some examples:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns. For example, if a bank offers a 5% interest rate on a savings account, you can easily calculate the interest earned on your deposits using percentage calculations.
-
Retail: Determining sale prices, markups, and discounts. Retailers frequently use percentages to advertise discounts ("20% off all items!") and calculate their profit margins based on the cost price and selling price of goods.
-
Statistics: Representing data, calculating proportions, and analyzing trends. Percentages are vital in presenting statistical data concisely and comparing different datasets. For instance, you might see that 75% of respondents in a survey favored a particular candidate.
-
Science: Expressing concentrations, analyzing experimental results, and expressing changes in quantities. In chemistry, for example, concentrations of solutions are often expressed as percentages (e.g., a 10% saline solution).
-
Everyday Life: Calculating tips, splitting bills, understanding nutrition labels, and interpreting statistics in news reports. We use percentages unconsciously in many daily activities, from calculating the tip at a restaurant to understanding the nutritional information on food packaging.
Solving More Complex Percentage Problems
The methods described above can be adapted to solve more complex percentage problems. For instance, consider the following:
-
What is 15% of 60? Here, we would use the formula: (Percentage/100) * Whole = Part. Therefore: (15/100) * 60 = 9.
-
If 25 is 40% of a number, what is the number? We can set up the proportion: 25/x = 40/100. Solving for x, we get x = 62.5.
-
What percentage increase is there from 50 to 75? First find the difference (75-50=25), then divide the difference by the original number (25/50=0.5), and finally multiply by 100 (0.5*100=50%). Therefore there is a 50% increase.
These examples demonstrate the versatility of percentage calculations and their applicability to a wide range of problems.
Common Mistakes to Avoid
While percentage calculations are relatively straightforward, there are a few common mistakes to avoid:
-
Incorrect Formula Usage: Ensure you use the correct formula based on the problem you're trying to solve. Confusing the "Part/Whole" relationship can lead to inaccurate results.
-
Calculation Errors: Double-check your calculations to avoid simple arithmetic errors. Using a calculator can help minimize this risk.
-
Misinterpreting the Question: Carefully read and understand the problem statement before attempting to solve it. Misunderstanding the question can lead to the wrong approach and an incorrect answer.
-
Rounding Errors: When dealing with decimals, be mindful of rounding errors. Carry extra decimal places during the calculation to minimize the impact of rounding on the final answer.
Conclusion
Determining what percentage of 20 is 16, which is 80%, provides a foundational understanding of percentage calculations. By mastering the various methods outlined in this article – the proportion method, the decimal method, and using a calculator – you will be well-equipped to tackle a wide range of percentage-related problems in various contexts. Remember to practice regularly, understand the underlying concepts, and be mindful of potential errors to develop proficiency in this essential mathematical skill. The ability to confidently calculate percentages is a valuable tool in many aspects of life, from personal finance to professional endeavors.
Latest Posts
Latest Posts
-
What Percent Of 16 Is 6
Apr 18, 2025
-
What Is The Lcm Of 6 And 14
Apr 18, 2025
-
How Many Inches Is 1 2 Cm
Apr 18, 2025
-
How Many Ounces In 237 Ml
Apr 18, 2025
-
How Many Species Go Extinct In An Average Day
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 20 Is 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.