What Percentage Of 30 Is 25
Kalali
Mar 09, 2025 · 4 min read
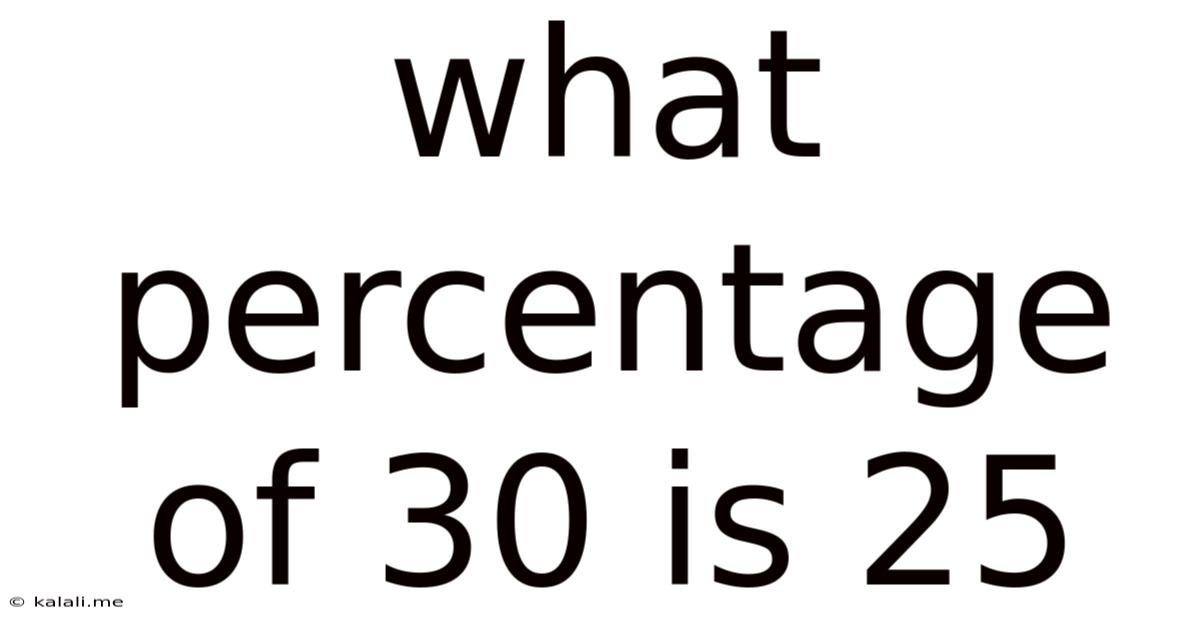
Table of Contents
What Percentage of 30 is 25? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to analyzing data and understanding financial reports. This article will delve into the question, "What percentage of 30 is 25?", providing a step-by-step explanation, exploring different approaches to solving this type of problem, and offering practical applications and examples.
Understanding Percentages:
A percentage is a fraction or ratio expressed as a portion of 100. The term "percent" literally means "out of one hundred." The symbol used to represent percentages is %. Percentages are used to express proportions, changes, and relationships between quantities. For example, 50% means 50 out of 100, or one-half.
Calculating What Percentage of 30 is 25:
There are several ways to calculate what percentage of 30 is 25. Let's explore the most common methods:
Method 1: Using Proportions
This method leverages the concept of proportions to solve the problem. We can set up a proportion where 'x' represents the unknown percentage:
25/30 = x/100
To solve for 'x', we cross-multiply:
30x = 2500
Then, divide both sides by 30:
x = 2500/30
x ≈ 83.33
Therefore, 25 is approximately 83.33% of 30.
Method 2: Using the Percentage Formula
The basic percentage formula is:
(Part/Whole) * 100 = Percentage
In our case:
Part = 25 Whole = 30
Substituting these values into the formula:
(25/30) * 100 = Percentage
0.8333 * 100 ≈ 83.33%
This confirms that 25 is approximately 83.33% of 30.
Method 3: Using Decimal Conversion
We can convert the fraction 25/30 into a decimal by dividing 25 by 30:
25 ÷ 30 ≈ 0.8333
Then, multiply the decimal by 100 to express it as a percentage:
0.8333 * 100 ≈ 83.33%
This method provides the same result: 25 is approximately 83.33% of 30.
Practical Applications and Examples:
Understanding percentage calculations has numerous real-world applications. Here are a few examples:
-
Sales and Discounts: A store offers a discount of $5 on an item originally priced at $30. To find the percentage discount, we use the same method: ($5/$30) * 100 ≈ 16.67%. The store is offering a 16.67% discount.
-
Grades and Assessments: A student scores 25 out of 30 on a test. Their percentage score is (25/30) * 100 ≈ 83.33%.
-
Financial Analysis: A company's profits increased from $25 million to $30 million. To calculate the percentage increase, we find the difference ($5 million), divide it by the original amount ($25 million), and multiply by 100: ($5/$25) * 100 = 20%. Profits increased by 20%.
-
Surveys and Statistics: In a survey of 30 people, 25 responded positively to a question. The percentage of positive responses is (25/30) * 100 ≈ 83.33%.
-
Tax Calculations: If the sales tax is 8%, and an item costs $30, the tax amount is 8% of $30: (8/100) * $30 = $2.40
Advanced Percentage Calculations:
While the above examples focused on finding the percentage, percentage problems can also involve finding the part or the whole, given the percentage and one of these other values. For instance:
-
Finding the Part: What is 83.33% of 30? This is solved by converting the percentage to a decimal (0.8333) and multiplying by 30: 0.8333 * 30 ≈ 25.
-
Finding the Whole: 25 is 83.33% of what number? Let's represent the unknown whole as 'y'. We can set up an equation: 0.8333y = 25. Solving for 'y', we divide both sides by 0.8333: y ≈ 30.
Importance of Accuracy and Rounding:
It's crucial to maintain accuracy throughout percentage calculations. However, in some cases, rounding is necessary to simplify the results. When rounding, remember to consider the context. In financial contexts, precise figures are usually essential. For general purposes, rounding to one or two decimal places is often sufficient.
Troubleshooting Common Mistakes:
Several common mistakes can arise when working with percentages:
-
Incorrect Formula Application: Ensure you are using the correct formula for the specific problem you're solving.
-
Decimal Errors: Errors often occur when converting between decimals and percentages. Double-check your decimal-to-percentage and percentage-to-decimal conversions.
-
Order of Operations: Follow the order of operations (PEMDAS/BODMAS) correctly, especially when dealing with multiple operations.
-
Rounding Errors: While rounding is sometimes necessary, excessive rounding can lead to inaccurate results. Minimize rounding until the final answer.
Conclusion:
Calculating percentages is a vital mathematical skill applicable across many fields. This comprehensive guide demonstrates how to determine what percentage of 30 is 25 using various methods and illustrates practical applications. By understanding the underlying principles and avoiding common errors, you can confidently tackle various percentage-related problems. Mastering percentage calculations empowers you to make informed decisions in various aspects of life, from personal finance to professional analysis. Remember to practice regularly and apply these concepts in real-world situations to strengthen your understanding and build confidence. Through consistent practice and a thorough understanding of the concepts, you can become proficient in handling percentage problems effectively.
Latest Posts
Latest Posts
-
A Warehouse Received 250 Orders In April
Jul 10, 2025
-
How Many Square Inches Are In 1 Square Foot
Jul 10, 2025
-
How Many Square Feet Is 3 4 Acre
Jul 10, 2025
-
How Many Centimeters Are In A Meter Stick
Jul 10, 2025
-
Why Did The Orchestra Get An R Rating
Jul 10, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 30 Is 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.