What Percentage Of 30 Is 6
Kalali
Apr 22, 2025 · 5 min read
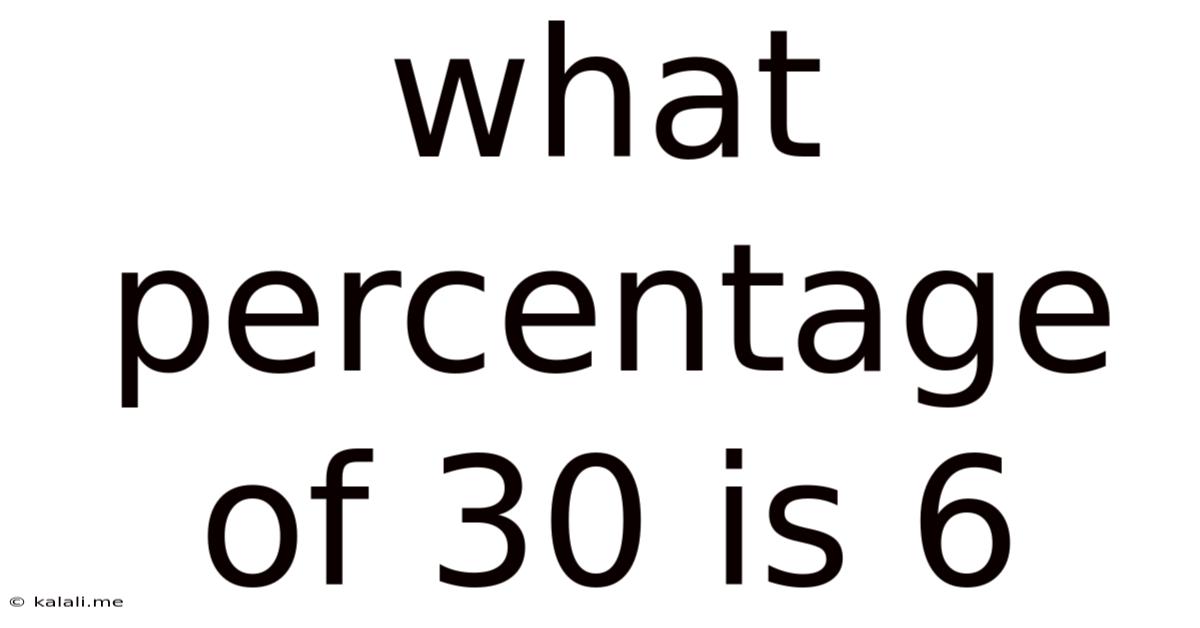
Table of Contents
What Percentage of 30 is 6? A Deep Dive into Percentage Calculations
This seemingly simple question, "What percentage of 30 is 6?", opens the door to a broader understanding of percentages, their applications, and the various methods used to calculate them. This article will not only answer the question directly but will also explore the underlying concepts, offer different approaches to solving percentage problems, and delve into real-world applications to solidify your understanding. By the end, you'll be equipped to confidently tackle any percentage calculation you encounter.
Meta Description: Learn how to calculate what percentage 6 is of 30. This in-depth guide explains the process, provides alternative methods, and explores real-world applications of percentage calculations. Master percentage problems with ease!
Understanding Percentages: The Fundamentals
Before we tackle the specific problem, let's establish a firm grasp of the fundamental concepts related to percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Percentages are incredibly versatile and used extensively in various fields, including:
- Finance: Calculating interest rates, discounts, profits, and losses.
- Statistics: Representing data proportions, probabilities, and survey results.
- Science: Expressing concentrations, efficiencies, and experimental yields.
- Everyday Life: Understanding sales, tips, and tax rates.
Method 1: Using the Formula
The most straightforward way to determine what percentage 6 is of 30 is to use the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 6 (the value we're interested in expressing as a percentage)
- Whole: 30 (the total value)
Plugging these values into the formula, we get:
(6 / 30) * 100% = 20%
Therefore, 6 is 20% of 30.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. A proportion is a statement that two ratios are equal. We can set up a proportion to solve for the unknown percentage (x):
6/30 = x/100
To solve for x, we cross-multiply:
6 * 100 = 30 * x
600 = 30x
x = 600 / 30
x = 20
Therefore, x = 20%, confirming our previous result. This method is particularly useful for visualizing the relationship between the parts and the whole.
Method 3: Using Decimal Equivalents
We can also approach this problem by first converting the fraction 6/30 into a decimal and then multiplying by 100% to express it as a percentage.
6/30 simplifies to 1/5. To convert 1/5 to a decimal, we divide 1 by 5:
1 ÷ 5 = 0.2
Now, multiply the decimal by 100% to get the percentage:
0.2 * 100% = 20%
Real-World Applications and Examples
Understanding percentage calculations is crucial for navigating various real-world scenarios. Here are a few examples:
-
Sales and Discounts: A store offers a 20% discount on an item originally priced at $30. The discount amount is 20% of $30, which we now know is $6. The final price would be $30 - $6 = $24.
-
Tax Calculations: If a 6% sales tax is applied to a $30 purchase, the tax amount would be (6/100) * $30 = $1.80. The total cost would be $30 + $1.80 = $31.80.
-
Grade Calculations: If a student answered 6 out of 30 questions correctly on a test, their score would be 20%. This helps in understanding their performance relative to the total number of questions.
-
Financial Investments: Calculating the return on investment (ROI) often involves percentage calculations. If an investment of $30 yields a profit of $6, the ROI is 20%.
-
Data Analysis: In statistical analysis, percentages are used to represent proportions within datasets. For instance, if a survey of 30 people shows that 6 prefer a particular product, then 20% of the surveyed population prefers that product.
Advanced Percentage Calculations: Beyond the Basics
While the problem "What percentage of 30 is 6?" is relatively straightforward, mastering percentage calculations requires understanding how to solve for different unknowns. For instance, you might encounter problems where you need to find the whole value given the percentage and the part, or find the part given the percentage and the whole.
Here's a summary of different scenarios and how to solve them:
Scenario 1: Finding the Percentage (As we did in the initial problem)
- Known: Part and Whole
- Unknown: Percentage
- Formula: (Part / Whole) * 100% = Percentage
Scenario 2: Finding the Part
- Known: Percentage and Whole
- Unknown: Part
- Formula: (Percentage / 100%) * Whole = Part
For example: What is 20% of 30? (20/100) * 30 = 6
Scenario 3: Finding the Whole
- Known: Percentage and Part
- Unknown: Whole
- Formula: (Part / Percentage) * 100% = Whole
For example: 6 is 20% of what number? (6 / 20) * 100 = 30
Tips for Mastering Percentage Calculations
-
Practice Regularly: The key to mastering any mathematical concept is consistent practice. Solve a variety of percentage problems to build your confidence and understanding.
-
Use Different Methods: Experiment with different approaches (formula, proportion, decimal equivalents) to find the method that works best for you.
-
Check Your Work: Always double-check your calculations to ensure accuracy. You can use a calculator to verify your results.
-
Understand the Context: Pay close attention to the wording of the problem to ensure you correctly identify the part, whole, and percentage.
-
Break Down Complex Problems: If you encounter a complex percentage problem, break it down into smaller, more manageable steps.
In conclusion, while the answer to "What percentage of 30 is 6?" is a simple 20%, the journey to understanding the solution unlocks a world of practical applications and mathematical skills. By mastering percentage calculations, you equip yourself with a valuable tool applicable across diverse fields and daily life. Remember to practice consistently, explore different methods, and always double-check your work. With practice, you'll become proficient in solving any percentage problem with confidence and ease.
Latest Posts
Latest Posts
-
2 Out Of 3 As A Percentage
Apr 22, 2025
-
How Many Liters In 64 Ounces
Apr 22, 2025
-
Cuanto Son 70 Grados Fahrenheit En Centigrados
Apr 22, 2025
-
Common Multiples Of 5 And 15
Apr 22, 2025
-
How Many Inches In 163 Cm
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 30 Is 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.